Achegándonos ao LHC
|
"Se hai unha cosa a facer é comprometerse coa educación". George Charpak (Premio Nobel en Física en 1992). |
|
El CERN celebra 70 años de descubrimientos científicos e innovación.
O Large Hadron Collider (Gran Colisor* de Hadróns) é o acelerador de partículas máis poderoso do mundo. O LHC (situado no noroeste da cidade suiza de Xenebra, sobre a fronteira Franco–Suiza) xera a maior cantidade de información nunca antes producida nun anterior experimento científico. O seu obxectivo é revelar algúns dos secretos fundamentais da natureza que quedan por descubrir.
(*) Sobre a utilización da palabra "colisor" ver...

A pesar da enorme cantidade de datos que podemos atopar sobre este acelerador e os seus experimentos, non é sinxelo para os non especialistas coñecer de onde proceden eses datos e o seu significado.
Basicamente, o propósito deste Sitio Web é esencialmente divulgativo tentando axudar a introducir este experimento ao público en xeral e ao alumnado e profesorado de ensino secundario en particular. Unha boa cantidade de cálculos son presentados para seren levados á clase de secundaria, estimulando a curiosidade dos estudantes, axudándolles así a comprender mellor algúns conceptos da Física. Preténdese que sexan un exemplo da relación entre as "frías" ecuacións da Física e o excitante mundo da investigación científica.
É importante suliñar que os cálculos que aparecen neste sitio web están adaptados ao nivel do ensino secundaria, e na maioría dos casos, aínda que e poidam resultar útiles, son simples aproximacións aos resultados correctos.
Amosamos deseguido algúns feitos que son de especial relevancia, aparecendo nas diferentes Seccións deste sitio web o desenvolvemento dos contidos e conceptos que consideramos de interese.
Se non estás familiarizado cos conceptos básicos da física de partículas, recomendámosche que visites primeiro as distintas seccións do menú xeral do noso sitio web.
Tamén presentamos as noticias máis recentes en Física de Partículas producidas no CERN. Na Sección Novas aparecen as noticias de anos anteriores.
CERN highlights en 2023
Tomado de CERN WEBSITE
Run 3
Ano 2022, comeza o LHC Run 3 despois dun vasto programa de traballos completados durante o Long Shutdown 2 (LS2). Os protóns coliden á máis alta enerxía (13.6 comparado con 13 TeV) e con máis luminosidade (contendo ata 1.8 × 1011 protones por bunch, comparado con 1.3–1.4 × 1011 ) que durante Run 2. Esta tercera fase experimental, Run 3, exténdese ata finais de 2025.
Esta terceira fase experimental esténdese ata o final de 2025.
Unhas poucas semanas despois do arranque do RUN3, varios récord foron xa alcanzados.
Algúns deles son:
.- enerxía con Pb iones: 6.8 Z TeV (ou 2.76 TeV/nucleón)
.- pico de luminosidade: 2.5·1034
.- pile-up (puntos de colisión casi simultáneos) > 100
.- enerxía almacenada por feixe: ~ 400 MJ
O calendario actural prevé o Long Shutdown 3 para comezar en 2026, un ano máis tarde que o que estaba previsto, e durará tres anos no canto de 2.5 anos (taken from CERN Courier).
Enerxía
Durante 2012 os protóns estiveron xirando cunha enerxía de 4 TeV por protón. En 2013 despois de ser utilizado para colisións con núcleos de Pb entrou e parada técnica (LS1) de arredor de 20 meses, para se reiniciar en 2015 as colisións cunha enerxía record de 6,5 TeV por protón. Despois de l Longa Parada (Long Shutdown 2, LS2) de 2019-2022, éntrase na tercera fase experimental, Run 3, coa máxima enerxía ata o de agora alcanzada - 6,8 TeV por proton - (13,6 TeV en colisión, moi perto xa da enerxía máxima de deseño inicial, 14 TeV).
Bosón de Higgs
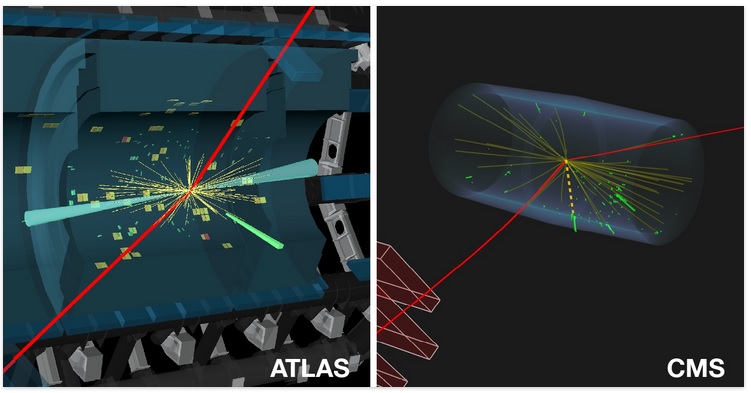
Con todo, un dos seus principais obxectivos, atopar o bosón de Higgs, foi xa acadado na fase inicial de operación. O Premio Nobel en Física 2013 foi otorgado a François Englert e Peter W. Higgs "polo descubrimento teórico dos mecanismo que contribúe á nosa comprensión da orixe da masa das partículas subatómicas, e que foi recentemente confirmado a partir do achádego da partícula fundamental asociada, nos experimentos ATLAS e CMS do Large Hadron Collider do CERN."
ATLAS e CMS anunciaron o descubrimento desa partícula o 4 de Xullo de 2012. Este resultado foi reconfirmado posteriormente en 2013.

Candidato Higgs decaendo en catro muóns rexistrado polo detector ATLAS en 2012 (Imaxe: ATLAS/CERN).
Artículos de interese sobre o Bosón de Higgs no décimo aniversario do seu descrubrimento, son os seguintes:
https://arxiv.org/abs/2207.
|
Precisamente no décimo aniversario do descubrimiento do Bosón de Higgs é un bo momento para sinalar que a investigación en Física de Partículas é tan necesaria como o ten sido sempre. Neste sentido é moi recomendable o seguinte artículo da revista Nature Particle physics isn’t going to die — even if the LHC finds no new particles Nature. 2022 Jul;607(7917):7-8. doi: 10.1038/d41586-022-01819-4. |
La CMS collaboration presentou a máis precisa medida do ángulo de mestura electrodébil.
Abril, 2024.
A colaboración CMS presentou (conferencia 2024 Rencontres de Moriond) a medida máis precisa do ángulo de mestura electrodébil leptónico efectivo realizada nun colisor de hadroóns ata a data, en bo acordo coa predición do Modelo Estándar.
 O ángulo de mestura electrodébil é un elemento crave destas comprobacións de consistencia. É un parámetro fundamental do Modelo Estándar, que determina como a interacción electrodébil unificada deu lugar ás interaccións electromagnética e débil a través dun proceso coñecido como ruptura de simetría electrodébil. Ao mesmo tempo, vincula matematicamente as masas dos bosones W e Z que transmiten a interacción débil. Así pois, as medidas do W, o Z ou o ángulo de mestura proporcionan unha boa comprobación experimental do Modelo.
O ángulo de mestura electrodébil é un elemento crave destas comprobacións de consistencia. É un parámetro fundamental do Modelo Estándar, que determina como a interacción electrodébil unificada deu lugar ás interaccións electromagnética e débil a través dun proceso coñecido como ruptura de simetría electrodébil. Ao mesmo tempo, vincula matematicamente as masas dos bosones W e Z que transmiten a interacción débil. Así pois, as medidas do W, o Z ou o ángulo de mestura proporcionan unha boa comprobación experimental do Modelo.
Medida da masa e o "ancho" (width, Γ𝑊) do bosón W co detector ATLAS.
Abril 2024
Os datos protón-protón rexistrados polo detector ATLAS en 2011, a unha enerxía de centro de masa de 7 TeV, utilizáronse para unha determinación mellorada da masa do bosón W e unha primeira medida da anchura do bosón W no LHC.
A “anchura” (width) dunha partícula está directamente relacionada co seu tempo de vida e describe como decae noutras partículas. Se o bosón W decae de forma inesperada, por exemplo en novas partículas aínda por descubrir, isto influirá na anchura medida.
Utilizando datos de colisións protón-protón a unha enerxía de 7 TeV recolleitos durante a primeira fase do LHC, ATLAS mediu a anchura do bosón W en 2202 ± 47 MeV. Trátase da medida máis precisa realizada ata a data por un só experimento e, aínda que un pouco maior, coincide coa predición do Modelo Estándar cunha precisión de 2,5 desviacións estándar.
A medida actualizada da masa do bosón W é de 80367 ± 16 MeV, que mellora e supera a medida anterior de ATLAS utilizando o mesmo conxunto de datos. Os valores medidos tanto da masa como da anchura coinciden coas predicións do Modelo Estándar.
LHCb collab: Medida da mestura D0− D0 e violación CP en D0➝ K+π− decays.
Marzo, 2024
Nun seminario celebrado o 26 de marzo no CERN, a colaboración LHCb do Gran Colisionador de Hadrones (LHC) presentou os resultados da súa última procura de asimetría materia-antimateria na oscilación do mesón neutro D, que, de atoparse, podería axudar a lanzar luz sobre o misterioso desequilibrio materia-antimateria do universo.Primera observación de fotones-a-taus en colisiones protón-protón en CMS.
Marzo, 2024
CMS Collaboration anuncia a observación de dous fotóns creando dous leptóns tau en colisións protón-protón. É a primeira vez que este proceso é observado en colisións pp, sendo posible grazas á capacidade de seguimiento de trazas do detector CMS.

Evento candidato del proceso γγ →ττ en colisiones protón–protón.
Tamén se reporta a máis precisa medida do momento magnético anómalo do leptón tau, ofrecendo unha nueva forma de restrinxir a existencia de nova física.
Tomado de CMS Collaboration Website.
Proba precisa da "universalidade do sabor leptónico" nas desintegracións de bosóns W en muóns e electróns.
Marzo, 2024
ATLAS Collaboration: Proeba precisa da universalidade do sabor leptónico en decaementos de bosóns W en muóns e electróns en colisións pp a √s=13 TeV co detector ATLAS. (58th Rencontres de Moriond 2024)
Un axioma fundamental do Modelo Estándar é a universalidad dos acoplamentos das diferentes familias de leptóns aos bosóns intermediarios da forza electrodébil. A medida da relación da taxa de desintegración de bosóns W a electróns e muóns, R(μ/e), constitúe unha proba importante deste axioma. Utilizando 140 fb−1 de colisións protón-protón rexistradas co detector ATLAS a una enerxía de centro de masas de 13 TeV, a Colaboración ATLAS informa dunha medida desta cantidade a partir de sucesos di-leptónicos nos que os quarks top decaen nun bosón W e un quark bottom.

O valor medido de R(μ/e) é 0,9995 ± 0,0045 e concorda coa hipótese de acoplamentos leptónicos universais postulada no Modelo Estándar. Trátase da única medición deste tipo realizada ata o de agora no Gran Colisor de Hadróns, e presenta o dobre de precisión cas medicións anteriores noutros aceleradores.
Observación da desintegración Bc+ → J/ψ J/ψ π+ π0
Xaneiro, 2024
LHCb Collaboration: A primeira observación do decaemento de Bc+ → J/ψ π+ π0 é reportada con alta significancia utilizando os datos de colisión protón-protón, correspondente a unha lumininosidade integrada de 9 fb-1, rexistrada polo detector LHCb con enerxías de centro de masas de 7, 8 e 13 TeV.
O mesón Bc+ (composto por dous quark pesados, b e c) é o mesón máis masivo que só pode decaer por interacción débil, vía o decaemento dun quark pesado constituinte (ver diagrama). Este decaemento de Bc+ en J/ψ e un par π+π0 no fora observado antes, principalmente porque a reconstrución precisa do mesón de baixa enerxía π0 (a través do par de foóns en que se desintegra) é un reto moi grande nos procesos de colisión protón-protón do LHC.

Diagrama para o decaemento do mesón Bc+ no mesón J/ψ e en hadróns lixeiros
A gran cantidade de b-quarks producidos nas colisións do LHC e a excelencia do detector, permite á LHCb Collaboration o estudo en detalle da produción, vias de decaemento e propiedades do mesón Bc+. Desde o descubrimento do Bc+ no expeimento CDF do Tevatron collider (Fermilab-Chicago), 18 novos decaementos do Bc+ foron observados (con máis de cinco sigmas de desviación estándar), todas no LHCb.
Un exabyte de almacenamiento en disco no CERN
Septiembre, 2023
O CERN alcanza un exabyte (un millón de Terabytes) de capacidade de almacenamento no seu centro de datos. Polo tanto, supérase o limiar do millón de terabytes de espacio en disco.
O almacén de datos del CERN no só serve para os datos de Física do LHC, senón tamén para todo o espectro de experimentos e servizos que precisan xestión de datos en líña.

La primera observación de neutrinos en el LHC.
Agosto 2023.
Os neutrinos están dentro das partículas máis abundantes en el universo, pero observarlos es un reto enorme dado que apenas interaccionan con la materia.
Os neutrinos son abundantemente producidos na colisión de protóns en aceleradores como o LHC, pero ata o de agora non foran directamente observados.
As colaboracións FASER e SND@LHC son dous diferentes experimentos dedicados á detección de neutrinos, ambos os dous no LHC, nos que recentemente, e de xeito indipendente foron observados neutrinos procedentes da colisión de protóns. Desta maneira pódense abrir novas importantes líñas de investigación en Física de Partículas.
ATLAS establece un récord de precisión na masa do bosón de Higgs.
Xullo 2023.
Tomado do CERN Website.
O Modelo Estándar non predír a masa do bosón de Higgs, polo que se debe determinar mediante medidas experimentais. O seu valor determina a forza das interaccións do bosón de Higgs con outras partículas elementais e consigo mesmo. Un coñecemento preciso deste parámetro fundamental é clave para realizar cálculos teóricos precisos que, á súa vez, permitan aos físicos confrontar as súas medicións das propiedades do bosón de Higgs coas predicións do Modelo Estándar. As desviacións respecto a estas predicións indicarían a presenza de fenómenos novos ou inexplicables.
A nova medida de ATLAS combina dous resultados: unha nova medida da masa do bosón de Higgs baseada nunha análise da desintegración da partícula en dous fotóns de alta enerxía (a "canle difotón") e unha medida de masa anterior baseada nun estudo da súa desintegración en catro leptones (a "canle catro-leptón").
A nova medida na canle dos difotons, que combina as análises dos conxuntos completos de datos ATLAS das series 1 e 2 do LHC, deu como resultado unha masa de 125.220 millóns de electronvoltios (GeV) cunha incerteza de só 0,14 GeV (0,09%).
Primeira evidencia dun raro decaemento do bosón de Higgs nun bosón Z e un fotón.
Maio 2023
O Modelo Estándar predí que, se o bosón de Higgs ten unha masa de arredor de 125 GeV, aproximadamente o 0.15% dos bosóns de Higgs decaerán nun bosón Z e un fotón.
Pero algunhas teorías que van máis aló do Modelo Estándar predín unha tasa de decaemento diferente. A medición desta tasa de decaemento aporta valiosas ideas tanto sobre a física máis aló do Modelo Estándar como sobre a natureza do bosón de Higgs.
Nun novo estudo, ATLAS e CMS uniron forzas para maximizar os datos recollidos durante o Run 2 (2015-2018) incrementando significativamente a precisión estatística.
Esta colaboración tradúcese nun resultado para este decaemento do bosón de Higgs nun bosón Z e un fotón cunha desviación estándar de 1.9 por riba da predición do Modelo Estándar. O resultado ten unha significancia estadística de 3.4, que aínda está por debaixo de requerimento de 5 necesario para reclamar ol descubrimiento
Na súa Sesión 195 (Nov 2019) o CERN Council nomeou a Fabiola Gianotti, como Directora Xeral da Organización, para un segundo mandato. Este novo nomeamento vai do 1 de xaneiro de 2021 a decembro de 2025. Esta é a primeira vez na historia do CERN que a Dirección Xeral foi prorrogada para un segundo mandato completo.
Ademais das diferentes Seccións deste sitio, creemos de interese visitar outros sitios web para ter unha idea máis xeral da Física de Partículas. Por exemplo: La aventura de las Partículas, ou outros sitios que se indican na sección Educación.
Algúns dos datos e informacións, así como imaxes, teñen sido tomado dos diferentes websites do CERN, tendo sido solicitado e concedido o correspondente permiso pola administración do CERN. O uso que se fai neste Sitio Web dos diferentes materiais procedentes das publicaciones producidas por lo CERN segue estrictamente os termos de uso que a este respecto indica o CERN.
O resto das imaxes, gráficas, etc., non feitas por nós, foron tomadas como de "fair use". Se non é o caso, por favor, fágannolo saber para retiralas de inmediato.
Un Glosario con termos de Física de Partículas, en orde alfabética, é incluído na última sección.|
AUTORES Xabier Cid Vidal, Doctor en Física de Partículas (experimental) pola Universidad de Santiago (USC). Research Fellow in experimental Particle Physics no CERN, desde xaneiro de 2013 a decembroe de 2015. Estivo vencellado ao Depto de Física de Partículas da USC como becario "Juan de la Cierva", "Ramon y Cajal" (Spanish Postdoctoral Senior Grants), e Profesor Contratado Doutor. Desde 2023 é Profesor Titular de Universidade nese Departamento (ORCID). Ramon Cid Manzano, foi profesor de Fïsica y Química no IES de SAR (Santiago - España), e Profesor Asociado nol Departamento de Didáctica de Ciencias Experimentais da Facultade de Educación da Universidad de Santiago (España), ata oseu retiro en 2020. É licenciado en Física e en Química, e Doutor pola Universidad de Santiago (USC).(ORCID). |
CERN CERN Experimental Physics Department CERN and the Environment |
LHC |
NOTA IMPORTANTE
Toda a Bibliografía que foi consultada para esta Sección está indicada na Sección de Referencias
© Xabier Cid Vidal & Ramon Cid - rcid@lhc-closer.es | SANTIAGO |








