Acercándonos al LHC
"Si hay una cosa que hacer es comprometerse con la educación". George Charpak (Premio Nobel en Física en 1992). |
|
El CERN celebra 70 años de descubrimientos científicos e innovación.
El Large Hadron Collider (Gran Colisionador de Hadrones) es el acelerador de partículas más poderoso del mundo. El LHC (situado en el noroeste de la ciudad suiza de Ginebra, sobre la frontera Franco–Suiza) genera la mayor cantidad de información nunca antes producida en anterior experimento. Su objetivo es revelar alguno de los secretos fundamentales de la naturaleza que quedan por descubrir.

A pesar de la enorme cantidad de datos que podemos encontrar sobre este acelerador y sus experimentos, no es sencillo para los no especialistas conocer de donde proceden esos datos y su significado.
Basicamente, el propósito de este sitio web es esencialmente divulgativo, ayudando a introducir este experimento al público en general, y al alumnado y profesorado de enseñanza secundaria en particular. Una buena cantidad de cálculos son presentados para ser llevados a clase de secundaria, estimulando la curiosidad de los estudiantes, ayudándoles así a comprender mejor algunos conceptos de Física. Se pretende que sean un ejemplo de la relación entre las "frías" ecuaciones de la Física y el excitante mundo de la investigación científica.
Es importante señalar que los cálculos que aparecen en este sitio web están adaptados al nivel de enseñanza secundaria, y en la mayoría de los casos, aunque puedan resultar útiles, son simples aproximaciones a los resultados correctos.
Mostramos a continuación algunos hechos que son de especial relevancia, apareciendo en las diferentes Secciones de este sitio web el desarrollo de los contenidos y conceptos que consideramos de interés.
Si no estás familiarizado con los conceptos básicos de la física de partículas, te recomendamos que visites primero las distintas secciones del menú general de nuestro sitio web.
También presentamos las noticias más recientes en Física de Partículas producidas en el CERN. Enn la Sección Noticias se encuentran las noticias de años anteriores.
CERN highlights en 2023
Tomado de CERN WEBSITE
Run 3
Año 2022, comienza el LHC Run 3 después de un vasto programa de trabajos completados durante el Long Shutdown 2 (LS2). Los protones colisionan a más alta energía (13.6 comparado con 13 TeV en Run 2) y con más luminosidad (conteniendo hasta 1.8 × 1011 protones por bunch, comparado con 1.3–1.4 × 1011) que durante Run 2. Esta tercera fase experimental, Run 3, se extiende hasta finales de 2025.
Esta tercera fase experimental se extiende hasta el final de 2025.
Unas pocas semanas después del arranque del RUN3, varios récord fueron ya alcanzados.
Algunos de ellos son:
.- energía con Pb iones: 6.8 Z TeV (o 2.76 TeV/nucleón)
.- pico de luminosidad: 2.5·1034
.- pile-up (puntos de colisión casi simultáneos) > 100
.- energía almacenada por haz: ~ 400 MJ
El calendario actural prevé el comienzo del Long Shutdown 3 en 2026, un año más tarde que lo que estaba previsto, y durará tres años en lugar de 2.5 años (taken from CERN Courier)
Energía
En 2012 los protóns estuvieron girando con una energía de 4 TeV por protón. En 2013, después de un tiempo con colisiones con núcleos de Pb, entró en parada técnica de alrededor de 20 meses, para reiniciar a principios de 2015 las colisiones con una energía de 6,5 TeV por protón. Después de la Larga Parada (Long Shutdown 2, LS2) de 2019-2022, comienza la tercera fase experimental, Run 3, con la máxima energía hasta ahora alcanzada - 6,8 TeV por proton - (13,6 TeV en colisión, muy cerca ya de la energía máxima de diseño inicial, 14 TeV).
Bosón de Higgs
En cualquier caso, uno de sus principales objetivos, encontrar el bosón de Higgs, fue ya alcanzado en la fase inicial de operación.
El Premio Nobel de Física 2013 fue concedido a François Englert y Peter W. Higgs "por el descubrimento teórico de los mecanismo que contribuyen a nuestra comprensión del origen de la masa de las partículas subatómicas, y que ha sido recientemente confirmado a partir del hallazgo de la partícula fundamental asociada, en los experimentos ATLAS y CMS del Large Hadron Collider del CERN."
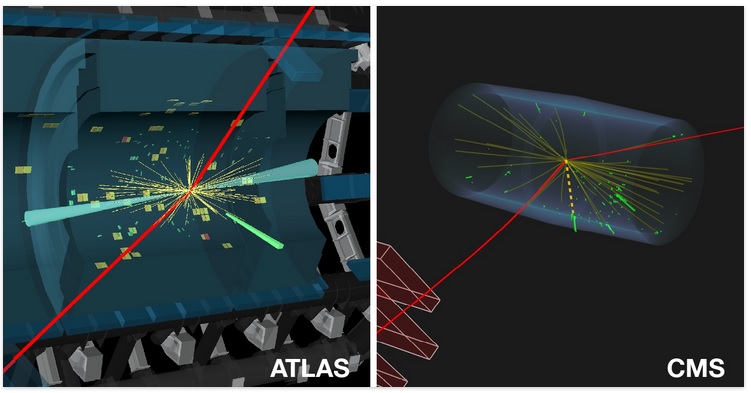
ATLAS y CMS anunciaron el descubrimiento de esa partícula el 4 de Julio de 2012. Este resultado fue reconfirmado posteriormente en 2013.

Candidato Higgs desintegrándose en cuatro muones registrado por ATLAS en 2012 (Imagen: ATLAS/CERN).
Artículos de interés sobre el Bosón de Higgs en el décimo aniversario de su descrubrimiento, son los siguientes:
|
Precisamente en el décimo aniversario del descubrimiento do Bosón de Higgs es un buen momento para señalar que la investigación en Física de Partículas es tan necesaria como lo ha sido siempre. En este sentido es muy recomendable el siguiente artículo de la revista Nature Particle physics isn’t going to die — even if the LHC finds no new particles Nature. 2022 Jul;607(7917):7-8. doi: 10.1038/d41586-022-01819-4. |
La CMS collaboration presentó la más precisa medida del ángulo de mezcla electrodébil.
Abril, 2024.
La colaboración CMS presentó (conferencia 2024 Rencontres de Moriond) la medida más precisa del ángulo de mezcla electrodébil leptónico efectivo realizada en un colisionador de hadrones hasta la fecha, en buen acuerdo con la predicción del Modelo Estándar.
 El ángulo de mezcla electrodébil es un elemento clave de estas comprobaciones de consistencia. Es un parámetro fundamental del Modelo Estándar, que determina cómo la interacción electrodébil unificada dio lugar a las interacciones electromagnética y débil a través de un proceso conocido como ruptura de simetría electrodébil. Al mismo tiempo, vincula matemáticamente las masas de los bosones W y Z que transmiten la interacción débil. Así pues, las medidas del W, el Z o el ángulo de mezcla proporcionan una buena comprobación experimental del Modelo.
El ángulo de mezcla electrodébil es un elemento clave de estas comprobaciones de consistencia. Es un parámetro fundamental del Modelo Estándar, que determina cómo la interacción electrodébil unificada dio lugar a las interacciones electromagnética y débil a través de un proceso conocido como ruptura de simetría electrodébil. Al mismo tiempo, vincula matemáticamente las masas de los bosones W y Z que transmiten la interacción débil. Así pues, las medidas del W, el Z o el ángulo de mezcla proporcionan una buena comprobación experimental del Modelo.
Medida de la masa y el "ancho" (width, Γ𝑊) del bosón W con el detector ATLAS.
Abril 2024.
Los datos protón-protón registrados por el detector ATLAS en 2011, a una energía de centro de masa de 7 TeV, se han utilizado para una determinación mejorada de la masa del bosón W y una primera medida de la anchura del bosón W en el LHC.
La “anchura” (width) de una partícula está directamente relacionada con su tiempo de vida y describe cómo decae en otras partículas. Si el bosón W decae de forma inesperada, por ejemplo en nuevas partículas aún por descubrir, esto influirá en la anchura medida.
Utilizando datos de colisiones protón-protón a una energía de 7 TeV recogidos durante la primera fase del LHC, ATLAS midió la anchura del bosón W en 2202 ± 47 MeV. Se trata de la medida más precisa realizada hasta la fecha por un solo experimento y, aunque un poco mayor, coincide con la predicción del Modelo Estándar con una precisión de 2,5 desviaciones estándar.
La medida actualizada de la masa del bosón W es de 80367 ± 16 MeV, que mejora y supera la medida anterior de ATLAS utilizando el mismo conjunto de datos. Los valores medidos tanto de la masa como de la anchura coinciden con las predicciones del Modelo Estándar.
LHCb collab: Medida de la mezcla D0− D0 y violación CP en D0➝ K+π− decays.
Marzo, 2024
En un seminario celebrado el 26 de marzo en el CERN, la colaboración LHCb del Gran Colisionador de Hadrones (LHC) presentó los resultados de su última búsqueda de asimetría materia-antimateria en la oscilación del mesón neutro D, que, de encontrarse, podría ayudar a arrojar luz sobre el misterioso desequilibrio materia-antimateria del universo.
Las oscilaciones de los mesones D0 e identifican como pequeños cambios en la mezcla de sabores (materia o antimateria) de los mesones D0 en función del momento en que decaen. La desintegración Kπ, de la que se ha informado hoy, es uno de los mejores canales para estudiar esta mezcla.
Los resultados concuerdan con los de estudios anteriores, confirmando la oscilación materia-antimateria del mesón D neutro y no mostrando indicios de violación CP en la oscilación. Los resultados invitan a futuros análisis de esta y otras desintegraciones del mesón D neutro utilizando los datos del tercero Run del LHC y su actualización prevista, el LHC de Alta Luminosidad.
Más aquí...Primera observación de fotones-a-taus en colisiones protón-protón en CMS.
Marzo, 2024
CMS Collaboration anuncia la observación de dos fotones creando dos leptones tau en colisiones protón-protón. Es la primera vez que este proceso ha sido visto en colisiones pp, siendo posible gracias a la capacidad de seguimiento de trazas del detector CMS.

Evento candidato del proceso γγ →ττ en colisiones protón–protón.
También se reporta la más precisa medida del momento magnético anómalo del leptón tau, ofreciendo una nueva forma de restringir la existencia de nueva física.
Tomado de CMS Collaboration Website.
Prueba precisa de la "universalidad del sabor leptónico" en las desintegraciones de bosones W en muones y electrones.
Marzo, 2024
ATLAS Collaboration: Prueba precisa de la universalidad del sabor leptónico en decaimientos de bosones W en muones y electrones en colisiones pp a √s=13 TeV con el detector ATLAS. (58th Rencontres de Moriond 2024)
Un axioma fundamental del Modelo Estándar es la universalidad de los acoplamientos de las diferentes familias de leptones a los bosones intermediarios de la fuerza electrodébi. La medida de la relación de la tasa de desintegración de bosones W a electrones y muones, R(μ/e), constituye una prueba importante de este axioma. Utilizando 140 fb−1 de colisiones protón-protón registradas con el detector ATLAS a una energía de centro de masa de 13 TeV, la Colaboración ATLAS informa de una medida de esta cantidad a partir de sucesos di-leptónicos en los que los quarks top decaen en un bosón W y un quark bottom.

El valor medido de R(μ/e) es 0,9995 ± 0,0045 y concuerda con la hipótesis de acoplamientos leptónicos universales postulada en el Modelo Estándar. Se trata de la única medición de este tipo realizada hasta ahora en el Gran Colisionador de Hadrones, y presenta el doble de precisión que las mediciones anteriores en otros aceleradores.
Observación de la desintegración Bc+ → J/ψ J/ψ π+ π0
Enero, 2024
LHCb Collaboration: La primera observación del decaimiento de Bc+ → J/ψ π+ π0 es reportada con alta significancia utilizando los datos de colisión protón-protón, correspondiente a una lumininosidad integrada de 9 fb-1, registrada por el detector LHCb con energías de centro de masas de 7, 8 y 13 TeV.
El mesón Bc+ (compuesto por dos quark pesados, b y c) es el mesón más masivo que solo puede decaer por interacción débil, vía el decaimiento de un quark pesado constituyente (ver diagrama). Este decaimiento de Bc+ en J/ψ y un par π+π0 no había sido observado antes, principalmente porque la reconstrucción precisa del mesón de baja energía π0 (a través de del par de fotones en que se desintegra) es un reto muy grande en los procesos de colisión protón-protón del LHC.

Diagrama para el decaimiento del mesón Bc+ en el mesón J/ψ y en hadrones ligeros
La gran cantidad de b-quarks producidos en las colisiones del LHC y la excelencia del detector, permite a la LHCb Collaboration el estudio en detalle de la producción, vias de decaimiento y propiedades del mesón Bc+. Desde el descubrimiento del Bc+ en el experimento CDF del Tevatron collider (Fermilab-Chicago), 18 nuevos decaimientos del Bc+ han sido observados (con más de cinco sigmas de desviación estándar), todas en el LHCb.
Un exabyte de almacenamiento en disco en el CERN
Septiembre, 2023
El CERN alcanza un exabyte (un millón de Terabytes) de capacidad de almacenamiento en su centro de datos. Por tanto, se supera el umbral del millón de terabytes de espacio en disco.
El almacén de datos del CERN no sólo sirve para los datos de Física del LHC, sino también para todo el espectro de experimentos y servicios que necesitan gestión de datos en línea.

La primera observación de neutrinos en el LHC.
Agosto 2023.
Los neutrinos están dentro de las partículas más abundantes en el universo, pero observarlos es un reto enorme dado que apenas interaccionan con la materia.
Los neutrinos son abundantemente producidos en la colisión de protones en aceleradores como el LHC, pero hasta ahora non habían sido directamente observados.
Las colaboraciones FASER y SND@LHC son dos diferentes experimentos dedicados a la detección de neutrinos, ambos en el LHC, en los que recientemente, y de forma indipendiente han sido observados neutrinos procedentes de la colisión de protones. De esta manera se pueden abrir nuevas importantes líneas de investigación en Física de Partículas.
ATLAS establece un récord de precisión en la masa del bosón de Higgs.
Julio 2023
Tomado del CERN Website.
El Modelo Estándar no predice la masa del bosón de Higgs, por lo que debe determinarse mediante medidas experimentales. Su valor determina la fuerza de las interacciones del bosón de Higgs con otras partículas elementales y consigo mismo. Un conocimiento preciso de este parámetro fundamental es clave para realizar cálculos teóricos precisos que, a su vez, permitan a los físicos confrontar sus mediciones de las propiedades del bosón de Higgs con las predicciones del Modelo Estándar. Las desviaciones respecto a estas predicciones indicarían la presencia de fenómenos nuevos o inexplicables.
La nueva medida de ATLAS combina dos resultados: una nueva medida de la masa del bosón de Higgs basada en un análisis de la desintegración de la partícula en dos fotones de alta energía (el "canal diphoton") y una medida de masa anterior basada en un estudio de su desintegración en cuatro leptones (el "canal four-lepton").
La nueva medida en el canal de los difotones, que combina los análisis de los conjuntos completos de datos ATLAS de las series 1 y 2 del LHC, dió como resultado una masa de 125.220 millones de electronvoltios (GeV) con una incertidumbre de sólo 0,14 GeV (0,09%).
Primera evidencia de un raro decaimiento del bosón de Higgs en un bosón Z y un fotón.
Mayo 2023.
El Modelo Estándar predice que, si el bosón de Higgs tiene una masa de alrededor de 125 GeV, aproximadamente el 0.15% de los bosones de Higgs decaerán en un bosónZ y un fotón.
Pero algunas teorías que van más allá del Modelo Estándar preciden una tasa de decaimiento diferente. La medición de esta tasa de decaimiento aporta valiosas ideas tanto sobre la física más allá del Modelo Estándar como sobre la naturaleza del bosón de Higgs.
En un nuevo estudio, ATLAS y CMS han unido fuerzas para maximizar los datos recogidos durante el Run 2 (2015-2018) incrementando significativamente la precisión estadística.
Esta colaboración se traduce en un resultado para este decaimiento del bosón de Higgs en un bosón Z y un fotón con una desviación estándar de 1.9 por encima de la predicción del Modelo Estándar. El resultado tiene una significancia estadística de 3.4, la cual está aún por debajo de requerimiento de 5 necesario para reclamar el descubrimiento.
... y para saber sobre lo que se está preparando para el futuro ver HL-LHC: High Luminosity LHC y también The Future Circular Collider
CERN Council nombra a Fabiola Gianotti para su segundo mandato como Directora General del CERN.
En su Sesión 195 el CERN Council (Nov 2019) nombró a Fabiola Gianotti, como Directora General de la Organización, para un segundo mandato. Este nuevo nombramiento va del 1 de enero de 2021 a diciembre de 2025. Esta es la primera vez en la historia del CERN que la Dirección General ha sido prorrogada para un segundo mandato completo.
NOTAS IMPORTANTES
Toda la Bibliografía que ha sido consultada para cada Sección está indicada en la Sección de Referencias
Reiteramos que los cálculos que aparecen en este sitio web están adaptados al nivel de la enseñanza secundaria, y en la mayoría de los casos, aunque puedan resultar útiles en general, son simples aproximaciones a los resultados correctos.
Además de las diferentes Secciones de este sitio, creemos de interés visitar otros sitios web para tener una idea más general de la Física de Partículas. Por ejemplo: La aventura de las Partículas, u otros sitios que se indican en la sección Educación.
Algunos de los datos e informaciones, así como imágenes, has sido tomados de los diferentes websites del CERN, habiendo sido solicitado y concedido el correspondente permiso para ello por la administración del CERN. El uso que se hace en este Sitio Web de los diferentes materiales procedentes de las publicaciones producidas por el CERN sigue estrictamente los términos de uso que a este respecto indica el CERN.El resto de las imágenes, gráficas, etc., no hechas por nosotros, han sido tomadas como de "fair use". Si no es el caso, por favor, hágannolo saber para retirarlas de inmediato.
Un Glosario con término de Física de Partículas, en orde alfabético, está incluído en la última sección.
|
AUTORES Xabier Cid Vidal, Doctor en Física de Partículas (experimental) por la Universidad de Santiago (USC). Research Fellow in experimental Particle Physics en el CERN, desde enero de 2013 a diciembre de 2015. Estuvo vinculado al Depto de Física de Partículas de la USC como becario "Juan de la Cierva", "Ramon y Cajal" (Spanish Postdoctoral Senior Grants), y Profesor Contratado Doctor. Desde 2023 es Profesor Titular de Universidad en ese Departamento (ORCID). Ramon Cid Manzano, profesor de Fïsica y Química en el IES de SAR (Santiago - España), y Profesor Asociado en el Departamento de Didáctica de Ciencias Experimentales de la Facultad de Educación de la Universidad de Santiago (España), hasta su retiro en 2020. Es licenciado en Física y en Química, y Doctor por la Universidad de Santiago (USC).(ORCID). |
CERN |
LHC |
NOTA IMPORTANTE
Toda la Bibliografía que ha sido consultada para esta Sección está indicada en la Sección de Referencias
© Xabier Cid Vidal & Ramon Cid - rcid@lhc-closer.es | SANTIAGO (ESPAÑA) |








