Taking a closer look at LHC
Particle responds to a force due to the presence of another particle because both two have thesame kind of charge.
This charge is a quantity carried by particles that determines their participation in an interactions process. A particle with electric charge has electrical interactions; one withstrong charge (or color charge) has strong interactions, one with weak charge (isospin or hypercharge) has weak interaction and inertial charge (mass) determines gravitational interaction.
One consequence of Heisenberg's uncertainty principle is that the energy and duration of a particle are also characterized by complementary uncertainties. There is always, at every point in space and time, even in a perfect vacuum, an uncertainty in energy and an uncertainty in duration, and these two complementary uncertainties cannot be reduced to zero simultaneously.
ΔE·Δt ~ ℏ ⇒ ΔE~ ℏ/Δt ⇒ Δm·c2~ ℏ/Δt
Δm ~ ℏ/(Δt·c2) (1)
A particle with mass = Δm can exist if its duration is less than Δt .
|
The meaning of Heisenberg's uncertainty principle is that "something" can arise from "nothing" if the "something" returns to the "nothing" after a very short time—an interval too short in which to be observed. These micro-violations of energy conservation are not only allowed to happen,they do, and so "empty" space is seething with particle-antiparticle pairs that come into being and then annihilate each other again after a very short interval.
The figure shows an interaction beetwen two electrons "using" a virtual photon (Feynman diagram).
Although these particles -VIRTUAL PARTICLES- cannot be observed individually , their existence can be demonstrated.
|
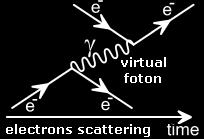 |
According (1), the more energy virtual particle ‘borrows’ from de vacuum (so the more mass they have) the shorter the time they can exist.
For each interaction there is a carrier particle (fundamental boson) associated with quantum excitations of the force field corresponding to that interaction. They are virtual particles that form out of vacuum field, as it was said above.
Because photon and graviton are massless the electromagnetic and gravitational interaction can reache infinite distance. However, the big masa of carrier particles for weak interaction implies very short duration and very short distance. The case of strong interaction is differentand it's related to the special characterisitics of the strong charge.
Gluons are carrier particles for strong interactions (color force fields), photons are carrier particles of electromagnetic interactions, the W and Z bosons are carrier particles for weak interactions, and gravitons are proposed as carrier particle for gravitational interaction.
The next animation shows a muon decay through a virtual W
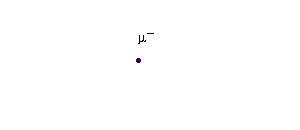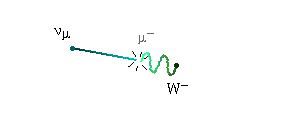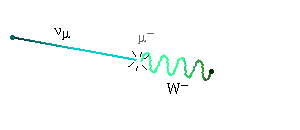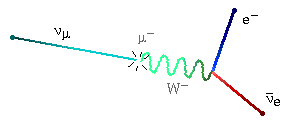
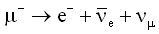

In regard to the gravitational interaction, we know that its unification with quantum theory is one of the most important challenges of fundamental physics.
As we know, the neutrino can have three fundamental configurations-flavors as they are termed in Particle Physics-which are electron, muon, and tau. Which of these configurations we observe changes as the neutrino travels, a truly strange phenomenon known as neutrino oscillations. This quantum behaviour is maintained over thousands of kilometres or more, which is referred to as quantum coherence.
Neutrino oscillations at the highest energies can be used to study the structure of spacetime and test the fundamental principles of quantum mechanics. If the spacetime metric has a quantum description, neutrinos are expected to interact with quantum fluctuations of that metric, deviating from the expected oscillatory flavour composition at long distances and high energies.

Image from ICECube Website
The IceCube Neutrino Observatory situated next to the Amundsen-Scott South Pole Station in Antarctica, is aimed to study these deviations.
|
AUTHORS Xabier Cid Vidal, PhD in experimental Particle Physics for Santiago University (USC). Research Fellow in experimental Particle Physics at CERN from January 2013 to Decembre 2015. He was until 2022 linked to the Department of Particle Physics of the USC as a "Juan de La Cierva", "Ramon y Cajal" fellow (Spanish Postdoctoral Senior Grants), and Associate Professor. Since 2023 is Senior Lecturer in that Department.(ORCID). Ramon Cid Manzano, until his retirement in 2020 was secondary school Physics Teacher at IES de SAR (Santiago - Spain), and part-time Lecturer (Profesor Asociado) in Faculty of Education at the University of Santiago (Spain). He has a Degree in Physics and a Degree in Chemistry, and he is PhD for Santiago University (USC) (ORCID). |
CERN CERN Experimental Physics Department CERN and the Environment |
LHC |
IMPORTANT NOTICE
For the bibliography used when writing this Section please go to the References Section
© Xabier Cid Vidal & Ramon Cid - rcid@lhc-closer.es | SANTIAGO (SPAIN) |



