Taking a closer look at LHC
The approach taken in this section is based on the article Introducing the Future Circular Collider (FCC) into Secondary Classrooms.
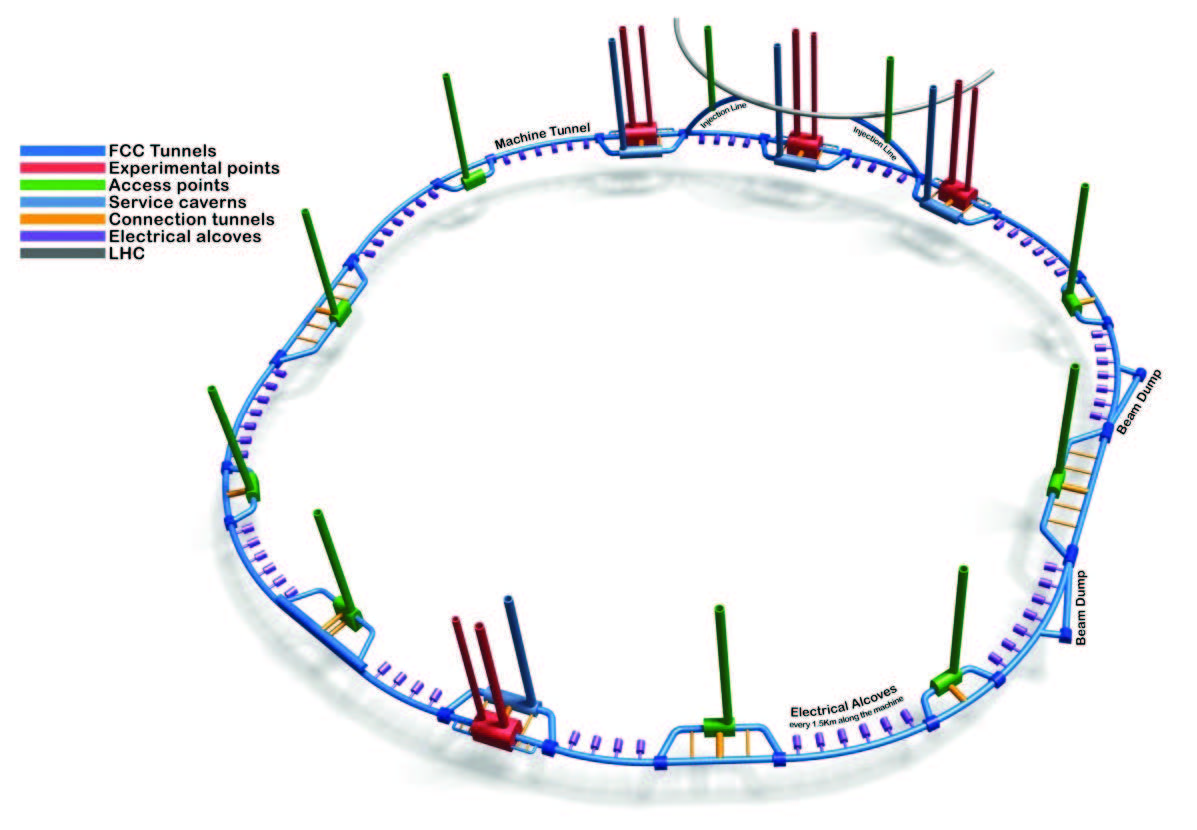
As we have also seen in the explanations on the LHC, FCC is not completely circular. It consists of straight parts inserted into arcs, in which the interaction points are installed (with detectors which register the events), particle injection zones (at high velocities, reached through previous accelerators), and extraction zones in which particle bunches -bunches- are retrieved when they do not present the necessary conditions for the required number of collisions that should occur at the interaction zones.
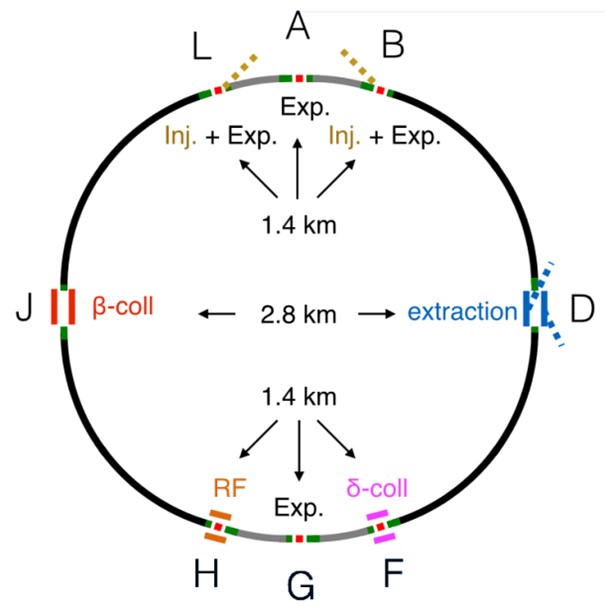
Fig 1. FCC-hh Layout (Image: CERN)
The “Bending radius (ρ)” is a defining parameter of a circular accelerator. It represents the radius of the theoretical circumference that the accelerator’s main arcs form. This parameter can be obtained approximately using simple Dynamics expressions. The centripetal force which curves the charged particles is the Lorentz Force:
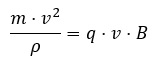
where B is the magnetic field of the magnetic dipoles which keep the charged particles in the arc’s curves.
Taking into account that these particles travel practically at the speed of light (v ≈ c), we get to:
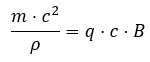
The numerator of the first term is the final energy (E) of the charged particle which travels through the accelerator. This means that:
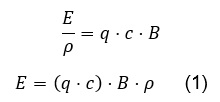
Both “q” and “c” are constants, which leads us to an important conclusion: the maximum energy that a charged particle can reach in a circular accelerator depends directly on the applied dipolar magnetic field (B) and the “Bending radius” (ρ):
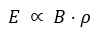
From expression (1) we have that:
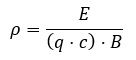
Using the values of “q” and “c” together with the appropriate conversion factors, we can obtain the value of ρ(km) from E (TeV) and B (T):
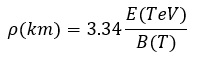
The marked goal for the FFC is obtaining 100 TeV energy at the centre of mass in a proton-proton collision (50 TeV per proton) assuming a 16 T dipolar magnetic field. This is already possible with technology which use Nb3Sn superconductor cables (*Benedikt and Zimmermann, 2018).
This leads to:
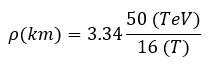
Therefore:
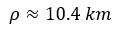
From this value we can deduce that the main arcs of the FCC form a curved zone with:
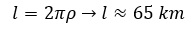
This curved part is divided in four big 16 km arcs (see Fig 1).
We should also consider the straight parts, which we referred to at the begging of this section, and the rest of the minor curved zones needed to connect the straight zones. The base dimension of the research implies an approximate 90 km long circular accelerator.
This value can be compared to the approximate 26,7 km of the current LHC. That is, we multiply the energy by 7, increasing the length by less than 3.5 times.
 |
 |
Images: CERN
More information about the FCC here and here.
*BENEDIKT M., ZIMMERMANN F. (2018). CERN thinks bigger. CERN Courier, 58 (5), 15-19 June, 2018. https://cerncourier.com/cern-thinks-bigger/
|
AUTHORS Xabier Cid Vidal, PhD in experimental Particle Physics for Santiago University (USC). Research Fellow in experimental Particle Physics at CERN from January 2013 to Decembre 2015. He was until 2022 linked to the Department of Particle Physics of the USC as a "Juan de La Cierva", "Ramon y Cajal" fellow (Spanish Postdoctoral Senior Grants), and Associate Professor. Since 2023 is Senior Lecturer in that Department.(ORCID). Ramon Cid Manzano, until his retirement in 2020 was secondary school Physics Teacher at IES de SAR (Santiago - Spain), and part-time Lecturer (Profesor Asociado) in Faculty of Education at the University of Santiago (Spain). He has a Degree in Physics and a Degree in Chemistry, and he is PhD for Santiago University (USC) (ORCID). |
CERN CERN Experimental Physics Department CERN and the Environment |
LHC |
IMPORTANT NOTICE
For the bibliography used when writing this Section please go to the References Section
© Xabier Cid Vidal & Ramon Cid - rcid@lhc-closer.es | SANTIAGO (SPAIN) |