Taking a closer look at LHC
In the LHC each proton reaches an energy of 7 TeV. Firstly, we introduce some basic calculations in Special Relativity and afterwards we present a more detailed calculation about energy of collisions in relativistic terms.
Let´s take a look at the relativistic parameter γ (gamma) when the proton reaches that energy.
|
In this case, the expression for Kinetic Energy is: Ek = γ·m0·c2 - m0·c2 o The mass of proton is 938,3 MeV/c2 So, m0·c2 = 9,383·10-4 TeV So (1): 7 TeV = 9,383·10-4 (γ-1) γ ~ 7460
γ>>1 , therefore we are nearing Special Relativity. We can now verify the of the proton with that energy comes close to that of the speed of light. In effect, γ = 1/[1- (v/c)2]1/2 with γ = 7460 ⇒ v = 0,999999991·c , so: v ~ c
|
 |
|
The use of energy units for other magnitudes is normal in the Physics of High Energies. Therefore the energy at rest of the proton will be: E0 =m0·c2 ⇒ E0 = 1,67·10-27kg·(3·108m/s)2 ⇒ E0 = 1,503·10-10 J Since, m0 = E0/c2 , the rest mass for the proton is: m0= 938,3 MeV/c2
That mass can also be expressed: m0=0,0009383 TeV/c2
|
|
|
Even though it´s a debatable concept that it will not be argued here, the energy reached by the proton in the LHC could be expressed as “relativistic mass”: m = E/c2 ⇒ m = 7 TeV/c2
Compare this value with m0=0,0009383 TeV/c2 to see the increase experimented. We could also get the value of the momentum of the proton in relative terms:
E2 = (p·c)2 + E02 ⇒ p·c = (E2 - E02)1/2 p·c = (72 - 0,00093832)1/2 ⇒ p ~ 7 TeV/c The value of the momentum of the proton is another important parameter in the accelerator.
|
|
|
|
|
|
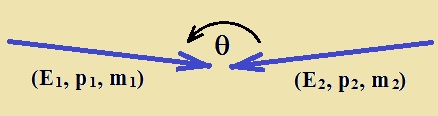
Energy in the Centre-of-Momentum Frame (COM frame). Consider the collision of two particles with energy, momentum and rest mass (E1, p1, m1) , (E2, p2, m2) at an incident angle Ɵ. The following quantity is an invariant (Lorentz invariant): s = (E1 +E2)2 - (c·p1 + c·p2)2 being p1 and p2 vectors and c = speed of light Operating on the above equation we have: s = (E12+ E22 + 2E1·E2) - (c2p12+c2p22 + 2p1c·p2c·cosƟ) Rearranging the terms: s = (E12 - c2p12) + (E22 - c2p22) + (2E1·E2 - 2p1c·p2c·cosƟ) Since (Ei2 - c2pi2) = (mi·c2)2 we have: s = (m1·c2)2 + (m2 c2)2 + 2(E1·E2 - p1c·p2c·cosƟ) [1] In Particle Physics is more common use the “natural units” (c = 1) . In this case, we have: s = (m1)2 + (m2)2 + 2(E1·E2 - p1·p2·cosƟ) The parameter “s” is so-called Mandelstam variable and “√s” corresponds to the energy in the COM frame, that is available for new particle production as a result of the collision. Fixed target vs Head-on collisions. 1.- Fixed target. Let m1 be the projectile and m2 the target. We have: p2 = 0 and E2 = m2 c2 , in COM frame. Then equation [1] gives: s = (m1·c2)2 + (m2·c2)2 + 2·E1· m2 c2 Take into account that E1 >> m1·c2 , m2 c2 , we have: s ~ 2E1·m2·c2
2.- Head-on collisions. Mass m1 and m2 in a head-on collision (Ɵ = 180º) cosƟ = -1 , so: s = (m1·c2)2 + (m2 c2)2 + 2(E1·E2 + p1c·p2c) Take into account that Ei >> mi·c2 and E1 ~ p1·c and E2 ~ p2·c , we have: s ~ 2(E1·E2·+ E1·E2) → s ~ 4E1·E2
For the special case of identicle particles of equal momentum, colliding head-on (like the case of LHC), the COM is at rest in the lab. We have, m1 = m2 = m and E1 = E2 = E . Then Then equation [1] gives: s = (m·c2)2 + (m c2)2 + 2(E·E + pc·pc) s = 2(m·c2)2 + 2·E2 + 2(p·c)2 s = 2[(m·c2)2 +(p·c)2] + 2·E2 but [(m·c2)2 +(p·c)2] = E2 so, s = 2·E2+ 2·E2 = 4·E2
So, in the case of p-p collision at LHC, with 7 TeV per proton: That is the energy available for new particle production in LHC collision. For a Fixed target, considering a proton moving with energy E1 colliding with a fixed target formed for a proton at rest (m2·c2 ~ 10-3 TeV) to get 14 TeV we need E1 to be: √s ~ √(2E1·m2·c2) 14 = √(2E1·10-3) E1 ~ 105 TeV It is very clear the advantage by using collider vs fixed target.
|
|
|
Finally, we could calculate the magnetic field present in the accelerator in another way visible in a previous section.
We have already calculated the bending radius (rb):
rb= 2804 m Fcentripetal = Fmagnetic ⇒ m·c2/rb = q·c·B
With, E = m·c2 ⇒ B = E/(c·q·rb) and since E = 7 TeV ⇒ E = 1,12·10-6 J So, B = 1,12·10-6/(3·108·1,602·10-19·2804)
B = 8,33 T
|
|
|
AUTHORS Xabier Cid Vidal, PhD in experimental Particle Physics for Santiago University (USC). Research Fellow in experimental Particle Physics at CERN from January 2013 to Decembre 2015. He was until 2022 linked to the Department of Particle Physics of the USC as a "Juan de La Cierva", "Ramon y Cajal" fellow (Spanish Postdoctoral Senior Grants), and Associate Professor. Since 2023 is Senior Lecturer in that Department.(ORCID). Ramon Cid Manzano, until his retirement in 2020 was secondary school Physics Teacher at IES de SAR (Santiago - Spain), and part-time Lecturer (Profesor Asociado) in Faculty of Education at the University of Santiago (Spain). He has a Degree in Physics and a Degree in Chemistry, and he is PhD for Santiago University (USC) (ORCID). |
CERN CERN Experimental Physics Department CERN and the Environment |
LHC |
IMPORTANT NOTICE
For the bibliography used when writing this Section please go to the References Section
© Xabier Cid Vidal & Ramon Cid - rcid@lhc-closer.es | SANTIAGO (SPAIN) |