Taking a closer look at LHC
(Next dicussion has basically been taken from Baird S. (2007). “ACCELERATORS FOR PEDESTRIANS”, AB-Note-2007-014 OP, CERN February 2007).
In order to study the proton motion, LHC mainly consists of dipole magnets to provide a closed circular path, quadrupole magnets to provide transverse focusing, and drift spaces.
As the protons move around the accelerator, whenever their divergence (angle) causes them to stray too far from the central trajectory the quadrupoles focus them back towards the central trajectory.
We characterise the position of the proton in this transverse motion by two things: Position or displacement from central path (x), and angle with respect to central path (x’).
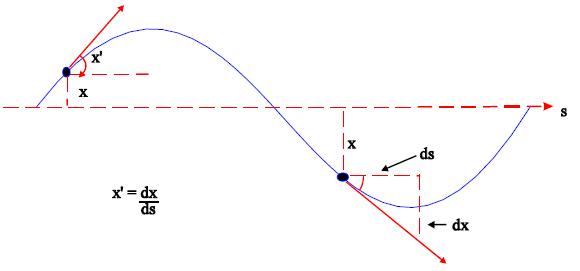
These transverse oscillations are called Betatron Oscillations, and they exist in both horizontal and vertical planes.
In first aproximation, we can express these transverse oscillations as varying in time:
d2x/dt2 + K·x = 0
Where K is de force constant taken here as a constant independent of s .
This is the equation of a SHM with solutions:
x = A·cos (ω·t + φ)
x’ = dx/dt ,, x’ = -Aω·sin (ω·t + φ)
The longitudinal speed of the particle is constant : v = s/t
so t = s/v → dt = ds/v and dx/dt = v·dx/ds
Therefore we can rewrite the solutions in function of s:
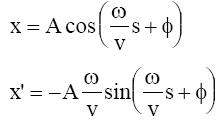
With many x,x’ “pairs” measured over many turns we can make a phase space plot: x vs x’.
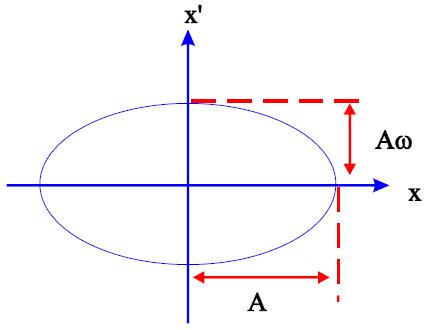
In reality our beam will consist of many particles each with different amplitudes A and different phases φ, so on any single turn we will see (if we could distinguish and measure each individual particle) many points on the above plot each corresponding to a particular particle.
But the focusing from the quadrupoles varies around the ring. In fact outside the quadrupoles there is no restoring force at all (K = 0).
So we have to consider K as function of s.
We can write a general equation for transverse motion:
d2x/ds2 + K(s)·x = 0
where K(s) is the focusing strength which is now a function of “s” and is no longer constant. This equation is called Hills equation.
To resolve it we introduce three parameters (ε, β(s) and ψ(s) ) which represent the behavior of the beam in function of the initial conditions (injection chain) and the focusing strength (quadrupoles).
ε = transversal emmitance, which is constant and depends on the initial conditions
β(s) = the amplitude modulation due to the changing focusing strength
ψ(s) = the phase advance, which also depends on focusing strength
With these parameters we can take a solution of the form:
![]() (1)
(1)
φ is the mathematical phase which depends on the initial conditions.
The rate of change of phase ψ(s) of the betatron oscillation around ring is proportional to the inverse of the particle’s oscillation amplitude. That is: dψ(s)/ds ~1/β(s) (2)
From (1) and (2), for the angle, x’, with x’ =dx/ds we get:
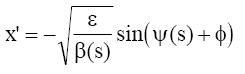
Next figure shows a plot in phase space of these x and x’ values over many turns for a single particle observed at one position, s, around the accelerator being β constant in this point.
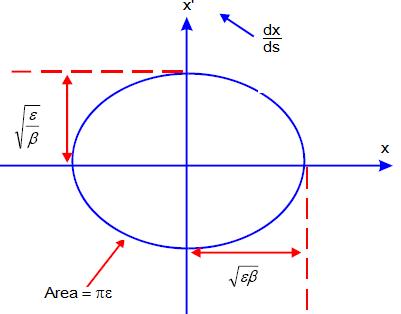
The transverse emittance, ε, has units of length (or length x angle), and is determined solely by initial conditions. However, as we move around the ring, β(s) varies and alters the shape of the ellipse, but the area of the ellipse remains constant all around the accelerator.
In fact to be rigorous we should define the emittance slightly differently. If we were able to observe all the particles at single position on one turn and measure both their position and angle, we would see a large number of points on our phase space plot, each corresponding to a pair of x,x’ values for each particle.
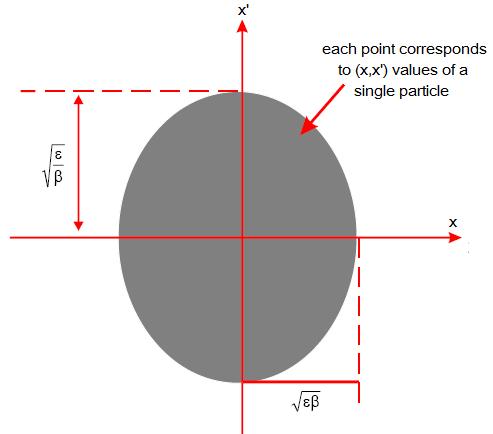
The emittance is the area of the ellipse which contains a certain percentage of the points or particles. We define a “95% emittance" as the area of ellipse which contains “95%” of the particles, or a "100% emittance" as the area which contains all the particles. Therefore when talking about a transverse emittance one must be sure of the definition being used. The projection of this ellipse onto the x axis will give the transverse size of beam. Therefore, the beam dimensions will vary as we move around the ring as β(s) varies.
The Beam dimension is:
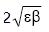
We can get the bunch cross section by doing the square of the Beam dimension:
cross section = 4 εβ
If we use σ (cross-sectional size average of the bunch) the cross section is 4πσ2
By comparing the two last equations we can express β in terms of σ and ε :
β =πσ2/ ε
Of particular significance is the value of the amplitude function at the interaction point (β*).Clearly one wants to be as small as possible; how small depends on the capability of the hardware to make a near-focus at the interaction point.
Other important kind of movement is the so called longitudinal oscillation.
The RF Cavities generate a longitudinal oscillanting voltage, which is applied across an isolated gap in the vacuum chamber, so that the particle sees an accelerating voltage at the gap, and the voltage then cancels out as the particle goes around the rest of the machine.
A particle exactly synchronised with the RF frequency is called synchronous particle. All the other particles in the accelerator will oscillate longitudinally around the synchronous particles under the influence of the RF system. This means that instead of being spread uniformly around the circumference of the accelerator the particles get “clumped” around the synchronous particle in a BUNCH.
These oscillations are called synchrotron oscillations.
You can follow a more complete explanation about this type of movement here...
|
AUTHORS Xabier Cid Vidal, PhD in experimental Particle Physics for Santiago University (USC). Research Fellow in experimental Particle Physics at CERN from January 2013 to Decembre 2015. He was until 2022 linked to the Department of Particle Physics of the USC as a "Juan de La Cierva", "Ramon y Cajal" fellow (Spanish Postdoctoral Senior Grants), and Associate Professor. Since 2023 is Senior Lecturer in that Department.(ORCID). Ramon Cid Manzano, until his retirement in 2020 was secondary school Physics Teacher at IES de SAR (Santiago - Spain), and part-time Lecturer (Profesor Asociado) in Faculty of Education at the University of Santiago (Spain). He has a Degree in Physics and a Degree in Chemistry, and he is PhD for Santiago University (USC) (ORCID). |
CERN CERN Experimental Physics Department CERN and the Environment |
LHC |
IMPORTANT NOTICE
For the bibliography used when writing this Section please go to the References Section
© Xabier Cid Vidal & Ramon Cid - rcid@lhc-closer.es | SANTIAGO (SPAIN) |



