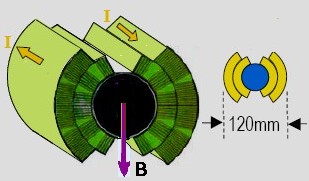
El campo magnético dipolar se crea gracias a sendas corrientes superconductoras que circulan sobre cada lado del tubo de vacío por donde viajan los protones. El cableado está dispuesto en sendas capas dobles alredor de cada tubo, circulando en sentidos contrarios a cada lado. Dado que el tubo tiene un diámetro de 56 mm, tomaremos, de acuerdo con las dimensiones que se indican, una distancia media desde el cableado al centro do tubo de 45 mm aproximadamente.

Los campos magnéticos creados por las corrientes de 11800 Amperios que circulan por los cables pueden ser calculados a partir da ley de Biot-Savart. B = μ0·I/(2πd) I ~11800 A  y   r ~ 45 mm,  así que en cada cable: B ~ 0.05 T El campo total necesario es de 8.33 T. Necesitamos:   8,33/0.05 ~ 160 cables

Es decir, para alcanzar los 8.33 T, necesitamos 160 cables superconductores (80 en cada lado) . Los ochenta cables, como ya se indicó, están situados en sendas capas dobles alredor de cada tubo, circulando la corriente en ellos en sentidos contrarios a cada lado del tubo.

Los cables están formados por 36 hilos de superconductores, cada un de los cuales tiene exactamente un diámetro de 0.825 mm. A su vez, cada hilo está formado por 6500 filamentos superconductores de Niobio-Titanio (47% de Ti).

Como cada dipolo cubre una distancia de unos 15 m podemos calcular a longitude total superconductora en los 1232 dipolos (2 tubos por dipolo):

L = 2 x 1232 x 160 x 36 x 6500 x 15   ⇒  L = 1,38·10¹² m

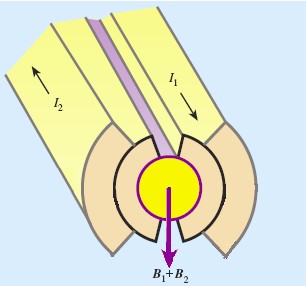
Dado que el sentido de la corriente en cada capa de cables es contraria a la de la otra, l os respectivos vectores B creados en el centro del tubo tienen el mismo sentido(sumándose por tanto). En el otro tubo los sentidos de las corrientes son los contrarios al que se acaba de describir, y por tanto, e campo total (B1+B2) creado en el centro de ese tubo tendrá el sentido contrario al del tubo vecino. Tenemos así la configuración 2-in-1 mencionada en la sección  Fuerza de Lorentz.

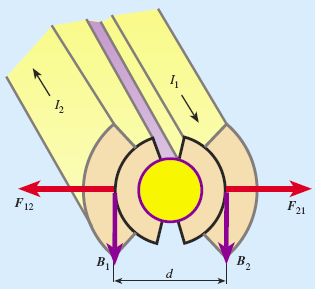
Por otra parte, sabemos que entre conductores paralelos aparecen fuerzas atractivas o repulsivas según sean los sentidos de las corrientes eléctricas que circulan por ellos. Como en este caso las corrientes sobre cada tubo van en sentido contrario, aparecerán fuerzas repulsivas entre las dos capas conductoras que rodean a ese tubo. Podemos utilizar la siguiente aproximación para calcular esa fuerza repulsiva por unidad de longitud de acuerdo con la fórmula: F/L = μ0·I1··I2/(2πd) Con  I ~11800 A  y   d = 90 mm, F/L = 310 N/m

Pero tenemos dos conjuntos de cableados con 80 cables en cada lado. Por tanto la fuerza por metro será: FT = 80·80·310 ~ 2·106 N/m Debido al diseño de las capas conductoras, esas fuerzas repulsivas actuarán principalmente en la dirección horizontal. Se trata de una intensa fuerza que tiende a “abrir” el dipolo. Para contrarrestar esa fuerza, los ingenieros rodean las capas conductoras con unos collares, hechos de acero inoxidable no magnético. Un núcleo hecho de hierro rodea los collares.

Vamos a calcular ahora la Inductancia del Dipolo Magnético.

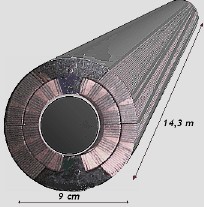
Consideraremos una "bobina cilíndrica" (14,3 m de larga y 90 mm de ancha -2 x 45 mm-), teniendo en cuenta aproximadamente las dimensiones reales) con 80 vueltas y un campo perpendicular de 8,33 T.

El Flujo magnético a través de la superficie que forma el "bobinado" es: φ = N·B·S   ⇒  φ = 80·8,33·(14,3·0,09)    φ ≈ 1000 Wb Con,    φ = L·I L = 1000/11800   ⇒     L ≈ 0.1 H Entonces, la energía almacenada en cada dipolo doble es: Ed  = ½·L·I2  ⇒  Ed ≈ 7 MJ Considerando 1232 dipolos: ET ≈ 9 GJ Suficiente para llevar a fusión total 45 Tm de Oro, desde 25 ºC.

Teniendo en cuenta su longitud, la densidad de energía en cada dipolo principal es:

7000/14,3 ≈ 500 kJ/m

Después de 10 h de colisiones, el haz de partículas debe ser extraído. El campo magnético de los dipolos magnéticos baja hasta los 0.54 T, permaneciendo así entre 20–40 min.  En este período de tiempo el proceso de inyección es repetido y los dipolos vuelven a alcanzar los 8.3 T para iniciarse otro ciclo de colisiones a alta energía. La máquina está diseñada para soportar unos 20000 ciclos de este tipo en 20 anos de vida útil

Comparación de dipolos desde el Tevatron al LHC.

Tomado de Lucio Rossi (2011): Superconductivity and the LHC: the early days

CERN COURIER OCT 2011