(La seguinte argumentación se ha tomado fundamentalmente de “ACCELERATORS FOR PEDESTRIANS” de Baird S. AB-Note-2007-014 OP, CERN February 2007).

A efectos de considerar los movimientos del protón, debemos fundamentalmente considerar  en el LHC los  imanes dipolares que aseguran la trayectoria circular, los imanes cuadrupolaresque proporcionan la focalización transversal, y zonas de deriva libre (drift spaces).

Mientras los protones se mueven en el acelerador, cualquiera que sea la distancia a la que se alejen de la trayectoria central serán redirigidos hacia esa trayectoria por acción de los imanes cuadrupolares. Esto genera un movimiento transversal de los protones además del longitudinal. 

Caracterizamos la posición del protón en su movimiento trasversal con dos parámetros:Posición o desplazamiento de la trayectoria central (x), y el ángulo con respecto a esa misma trayectoria (x’).

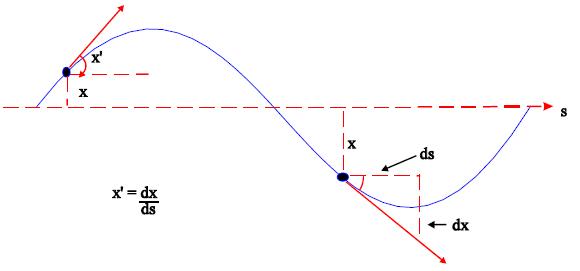
Las oscilaciones transversales son llamadas Oscilaciones Betatrón, y existen tanto en el plano horizontal como en el vertical.

En primera aproximación, podemos expresar esas oscilaciones transversales en función del tiempo:

d²x/dt² + K·x = 0

donde K es la constante de fuerza tomada aquí como constante e independiente de s .

Se trata de la ecuación de un MAS con las conocidas soluciones:

x = A·cos (ω·t + φ)

x’ = dx/dt ,,     x’ = -Aω·sin (ω·t + φ)

La velocidad longitudinal del protón es constante:  v = s/t

Tenemos pues   t = s/v   →   dt = ds/v    e   dx/dt = v·dx/ds

Por lo tanto podemos reescribir las soluciones en función de s:

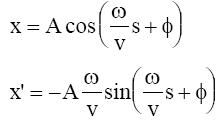
Con muchas parejas valores (x,x’) medidos sobre muchas vueltas podemos realizar la gráfica llamada espacio de fases: x vs x’.

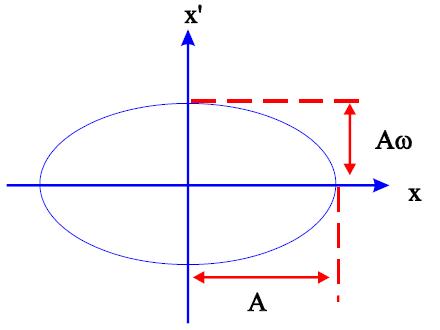
En realidad el haz consiste en muchas partículas con diferentes amplitudes A y diferentes fases φ. Se pudiésemos distinguir y medir cada partícula individual la gráfica anterior podría representar a una partícula concreta después de muchas vueltas.

Pero la focalización producida por los cuadrupolos varía a lo largo del acelerador. De hecho donde non hay cuadrupolos no hay fuerza restauradora en absoluto (K = 0).

Debemos, pues, considerar K como función de s. 

Escribimos entonces la ecuación general para elo movemento transversal:

d²x/ds² + K(s)·x = 0

donde K(s) es ahora función de “s” y por tanto ya no es constante. Esta ecuación es llamada ecuación de Hills .

Para resolverla introducimos tres parámetros (ε,  β(s) y ψ(s)) que representan el comportamiento del haz en función de las condicións iniciailes (cadena de inyección) y la intensidad focalizadora (cuadrupolos).

ε = emitancia transversal,  que es constante y depende de las condiciones iniciales

β(s) = modulación de amplitud, debido a los cambios en la fuerza focalizadora

ψ(s) = el avance de fase, que también depende de la intensidad focalizadora

Con estos parámetros podemos tomar como solución:

(1)

φ es la fase matemática que depende de las condicións iniciales.

La rapidez del cambio de la fase ψ(s) de estas oscilaciones alrededor del acelerador es proporcional al inverso de la amplitud de oscilación. Es decir:   dψ(s)/ds ~1/β(s)  (2)

Considerando (1) y (2), tenemos para el ángulo, x’, con x’ =dx/ds:

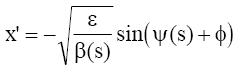
La siguiente figura del espacio de fases representa los valores x y x’ en varias vueltas para una partícula observada en una determinada posición, s, siendo en ese lugar β constante.

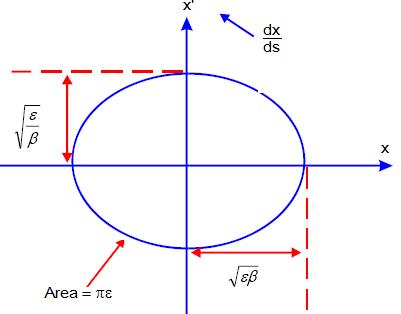
La emitancia transversal, ε, tieen unidades de longitud (o longitud x ángulo), y vienedeterminada únicamente por las condiciones iniciales. Sin embargo, cuando nos movemos alrededor del acelerador, β(s) varía y altera la forma de la elipse, pero el área de la elipse permanece constante a lo largo del acelerador. En efecto el área depende de ε que como se indicó es función sólo de las condiciones iniciales.

Pero para ser más riguroso deberemos definir la emitancia de una forma algo diferente. Si fuéseos capaz de observar todas las particulas en una determinada posición en una vuelta y medir tanto x como x', veríamos un gran número de puntos en la gráfica del espacio de fases.

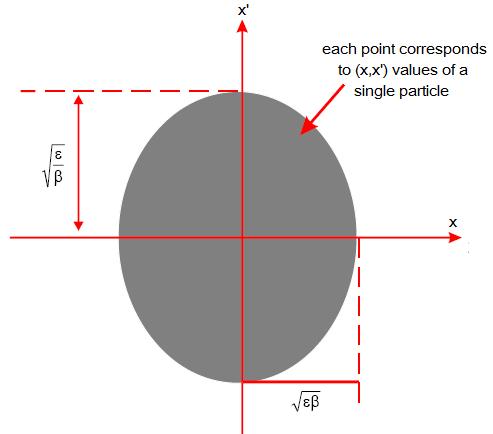
La emitancia es el área de la elipse la cual contiene un cierto porcentaje de puntos o partículas. Definimos una “emitancia al 95%" como el área de la elipse que contiene un “95%” de partículas, o una "emitancia al 100%" como el área de la elipse que contiene a todas las partículas. Por lo tanto cuando hablamos de emitancia transversal deberemos estar seguro de la definición utilizada. La proyección de esta elipse sobre el eje nos da el tamaño de la sección transversal del haz. Por tanto variará en el acelerador según varíe el valor de β(s).

De la figura vemos que el tamaño transversal del haz es:

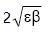
Podemos además obtener la sección transversal del bunch haciendo el cuadrado del tamaño transversal del haz: 

sección transversal = 4 εβ

Si consideramos σ (tamaño medio transversal del bunch) la sección transversal es 4πσ²

Comparando las dos últimas ecuaciones podemos expresar β en términos de σ y ε  :

 β = πσ²/ε

De particular importancia es el valor de la función de amplitud en el punto de interacción, β*.Obviamente este valor debe ser lo más pequeño posible, dependiendo esto de la capacidad del sistema de focalización en las proximidades del punto de interacción.

Otra importante clase de movimoento es la oscilación longitudinal. 

Las Cavidades RF generan un voltaje oscilante longitudinal, que es aplicada en  la cámara de vació exclusivamente, quedando nula en el resto de la máquina.

Una partícula exactamente sincronizada con esa frecuenca oscilante es llamada partícula síncrona. Todas las demás oscilan longitudinalmente alrededor de la síncrona bajo  ña influencia del sistema RF. Esto significa que en lugar de estar las partículas esparcidas uniformemente en la circunferencia del acelerador, se mueven en paquetes (bunches).

Esas oscllacioness lonxgitudinales se llaman oscilaciones sincrotrón.

Se puede seguir una explicación más completa aquí...