(A seguinte argumentación ten sido basicamente tomada de Baird S.  (2007).  “ACCELERATORS FOR PEDESTRIANS”, AB-Note-2007-014 OP, CERN February 2007).

A efectos de considerar os movementos do protón, debemos fundamentalmente considerar  noLHC os  imáns dipolares que aseguran a traxectoria circular, os imáns cuadrupolares que proporcionan a focalización transversal, e zonas de deriva libre (drift spaces).

Mentres os protóns se moven no acelerador, calquera que sexa a súa diverxencia que o afasta da traxectoria central serán redirixidos cara esa traxectoria por acción dos imáns cuadrupolares. Isto xera un movemento transversal dos protóns ademais do lonxitudinal. 

Caracterizamos a posición do protón no seu movemento trasversal con dous parámetros:Posición ou desprazamento da traxectoria central (x), e o ángulo con respecto a esa mesma traxectoria (x’).

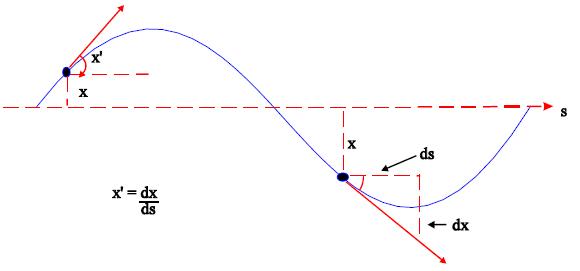
As oscilacións transversais son chamadas Oscilacións Betatrón, e existen tanto no plano horizontal e no vertical.

En primeira aproximación, podemos expresar esas oscilacións transversais en función do tempo:

d²x/dt² + K·x = 0

onde K é a constante de forza tomada aquí como constante e independente de s .

Trátase da ecuación dun MHS coas coñecidas solucións:

x = A·cos (ω·t + φ)

x’ = dx/dt ,,     x’ = -Aω·sin (ω·t + φ)

A velocidade lonxitudinal do protón é constante:  v = s/t

Temos pois   t = s/v   →   dt = ds/v    e   dx/dt = v·dx/ds

Polo tanto podemos reescribir as solucións en función de s:

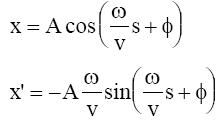
Con moitas parellas de valores (x,x’) medidos sobre moitas voltas podemos realizar a gráfica chamada espazo de fases: x vs x’.

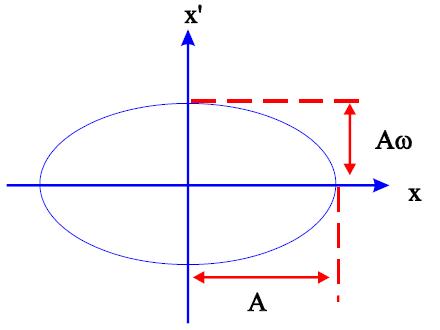
En realidade o feixe consiste en moitas partículas con diferentes amplitudes A e diferentes fases φ. Se poidésemos distinguir e medir cada partícula individual a gráfica anterior poderían representar a unha partícula concreta despois de moitas voltas.

Pero a focalización producida polos cuadrupolos varía ao longo do acelerador. De feito onde non hai cuadrupolos non hai forza restauradora en absoluto (K = 0).

Debemos, pois, considerar K como función de s. 

Escribimos entón a ecuación xeral para o movemento transversal:

d²x/ds² + K(s)·x = 0

onde K(s) é agora función de “s” e por tanto xa non é constante. Esta ecuación é chamada ecuación de Hills .

Para resolvela introducimos tres parámetros (ε,  β(s) and ψ(s)) que representan o comportamento do feixe en función das condicións iniciais (cadea de inxección) e  a intensidade focalizadora (cuadrupolos).

ε = emitancia transversal,  que é constante e depende das condicións iniciais

β(s) = modulación de amplitude, debido aos cambios na forza focalizadora

ψ(s) = o avance de fase, que tamén depende da intensidade focalizadora

Con estos parámetros podemos tomar como solución:

(1)

φ é a fase matemática que depende das condicións iniciais.

A rapidez do cambio da fase ψ(s) destas oscilacións arredor do acelerador é proporcional ao inverso da amplitude de oscilación. É dicir:   dψ(s)/ds ~1/β(s)  (2)

Considerando (1) e (2), temos para o ángulo, x’, con x’ =dx/ds:

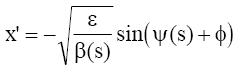
A seguinte figura do espazo de fases representa os valores x e x’ en varias voltas para unha partícula observada nunha determinada posición, s, sendo nese lugar β constante.

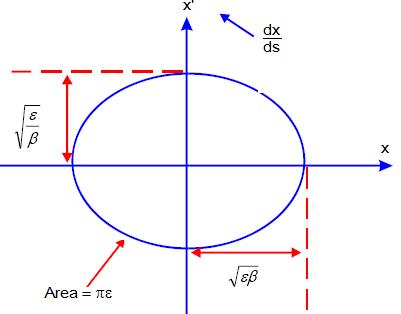
A emitancia transversal, ε, ten unidades de lonxitude (ou lonxitude x ángulo), e vendeterminada unicamente polas condicións iniciais. Porén, cando nos movemos arredor do acelerador, β(s) varía e altera a forma da elipse, pero a área da elipse permanece constanteao longo do acelerador. En efecto a área depende de ε que como se indicou é función só das condicións iniciais.

Pero para sermos máis riguroso deberemos definir a emitancia dunha forma algo diferente. Se fósemos quen de observar todas as particulas nunha determinada posición nunha volta e medir tanto x e x', veríamos un gran número de puntos na gráfica do espacio de fases.

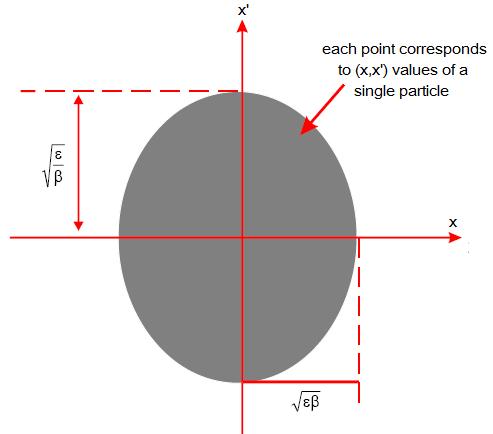
A emitancia é a área da elipse a cal contén unha certa porcentaxe de puntos ou partículas. Definimos unha “emitancia ao 95%" como o área da elipse que contén un “95%” de partículas, ou unha "emitancia ao 100%" como o área da elipse que contén a todas as partículas. Polo tanto cando falamos de emitancia transversal deberemos estar seguro da definición utilizada. A proxección desta elipse sobre o eixe xa  danos o tamaño da sección transversal do feixe. Polo tant a variará ao longo do acelerador segundo varíe o valor de β(s).

Da figura vemos que o tamaño transversal do feixe é:

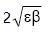
Podemos ademais achegarnos á sección transversal do bunch facendo o cadrado do tamaño transversal do feixe: 

sección transversal = 4 εβ

Se consideramos σ (tamaño medio transversal do bunch) a sección transversal é 4πσ²

Comparando as dúas últimas ecuacións podemos expresar  β en termos de σ e ε  :

 β = πσ²/ε

De particular importancia é o valor da función de amplitude no punto de interacción, β*.Obviamente este valor debe ser o máis pequeno posible, dependendo isto da capacidade do sistema de focalización nas proximidades do punto de interacción.

Outra importante clase de movmento é a oscilación lonxitudinal. 

As Cavidades RF xeran unha voltaxe oscilante lonxitudinal, que é aplicada na súa cámara de baleiro exclusivamente, quedando nula no resto da máquina.

Unha partícula exactamente sincronizada com esa frecuenca oscilante é chamada partícula síncrona. Todas as demais oscilan lonxitudinalmente arredor da síncrona baixo  a influencia do sistema RF. Isto significa que no canto de estaren as partículas espraiadas uniformemente na circunferencia do acelerador, móvemense en paquetes (bunches).

Esas oscllacións lonxitudinais chámasen oscilacións sincrotrón.

Pódese seguir unha explicación máis completa aquí...