Básicamente Linac4 funciona de la misma forma que cualquier acelerador lineal. Utiliza cavidades de radiofrecuencia que cargan eléctricamente conductores cilíndricos. Los iones H^- injectados desde la fuente de iones pasan a través de esos condictores, que son cargados alternativamente con carga positiva y negativa. Así, las partículas son empujadas desde atrás y atraídas hacia adelante, provocando su aceleración. Pequeños cuadrupolos magnéticos aseguran que el haz de iones hidrógeno se mantenga lo más compacto posible.

Algo de física en el LINAC 4.

Calculemos como los ions  H^- interactúan entre ellos mientras son acelerador, utilizando una aproximación sencilla.

Podemos considerar que el haz está compuesto por un infinito número de "líneas" (o "corrientes") de iones H^- presentes en el cilindro que representa el haz de iones. Podemos imaginarlo como un gran número de "espaguetis" con carga negativas que crean y sufren fuerzas eléctricas y magnéticas entre ellas.

Cada dos "líneas" de iones H^- viajando en l misma dirección con velocidade v y separados por una distancia r, experimentarán una fuerza mutua entre ellos que vamos a calcular.

En esta aproximación, cada partícula en una "línea" siente la Fuerza de Lorentz producida por la otra "línea":

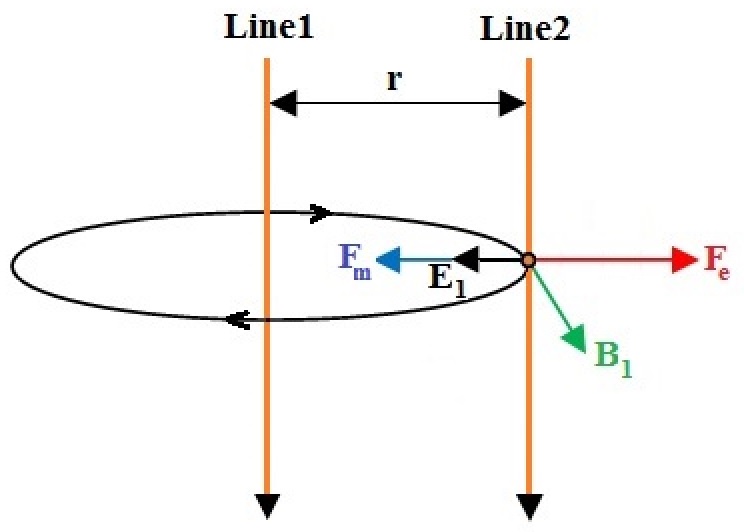
Ambas fuerzas creadas por la "línea 1" actúa sobre cada partícula de la "línea 2", pero con sentidos opuestos. Entonces:

El valor de E₁ actuando sobre cada partícula puede ser calculado usando el Teorema de Gauss (campo eléctrico a una distancia r creado por una corriente infinita):

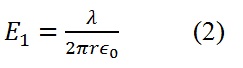
donde λ es  la "densidad lineal de carga".

El valor de B₁ puede ser calculado mediante la ley de Biot-Savart:

siendo I la intensidad de corriente en la "línea 1"

Tomando de nuevo λ, podemos sustituir I :

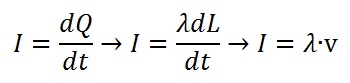
Tenemos enotnces para B₁:

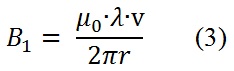
Llevando (2) y (3) a (1):

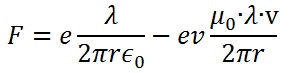
Recolocando los términos en la anterior expresión:

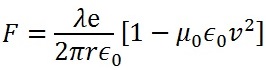
Dado que

tendremos

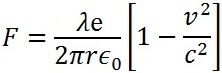
o

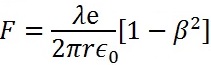
Y finalmente:

o

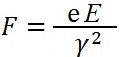
Vemos que la Fuerza neta de repulsión depende del valor de λ (o E), que limita entonces el número de partículas por paquete (o pulso). Pero dado el término (1/γ²), F decrece rápidamente en condiciones relativísticas.

Por tanto, cuanto más rápido vayan las partículas menor repulsión habrá entre ellas.