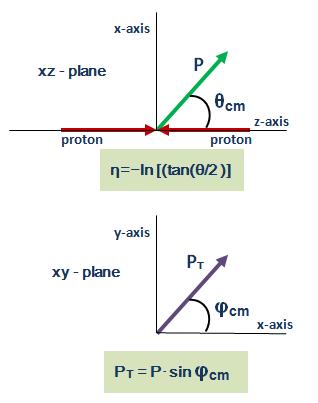
The momentum of a particle is the product of the mass and velocity: p = m·v = (px , py , px ) In spherical coordinates centered in collision point, p = (|p|, θ, φ), with θ as polar angle and φ as azimuthal angle. Since most detectors are cilinder, a new magnitude called pseudorapidity is used: η=−ln [(tan(θ /2)] with values between (−∞, ∞). In hadron collider physics, the pseudorapidity is preferred over the polar angle θ because, loosely speaking, particle production is constant as a function of pseudorapidity. Besides, transversal momentum, pT , is also prefered and it is calculated from transversal Energy, delivered on calorimeters. So, in Particle Physics linear momentum is represented by: p =( pT , η , φ). To obtain cartesian momenta (px , py , pz), with the z-axis as the beam axis, the following conversions are used:  px = pT·cosφ  py = pT·sinφ  pz = pT·sinhη and,   |p| = pT·coshη

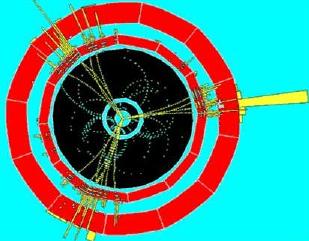
This first image shows a event of a collision in a detector.

The momentum conservation must be verified.

Since protons that collide head on have identic values of momentum -7 TeV/c- and practically opposite in direction (the two beams will meet at an angle about 200 mrad), the particles produced after collision must also have zero momentum.

This second image shows the detection of the jets of particles generated after collision of two particles which travelled in opposite directions and perpendicular to the image. Since the total momentum before collision is zero it will be zero after collision. This can be seen in the image.

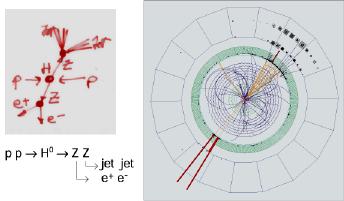
This third image represents the simulation of a very expected event in the LHC detectors and we can observe that the momentum conservation is verified. In the case that this event is confirmed the two particles Zº are created from Higgs particle, and we can see the production for two electrons and two jets of new particles. particle will be detected.

A charged particle moving in a B-field experiences a sideways force that is proportional to the strength of the magnetic field, the component of the velocity that is perpendicular to the magnetic field and the charge of the particle. This force is the Lorentz force, and is given by:

 F = q·[v x B]

With   v = v_ￌ + v_ǁ  (regard to B)   →                          F = q [(v_ￌ+v_ǁ) x B]

Then:                                                                            F = q·v_ￌ·B        (1)

The Lorentz force is always perpendicular to both the velocity of the particle and the magnetic field that created it. When a charged particle moves in a static magnetic field it will trace out a helical path in which the helix axis is parallel to the magnetic field and in which the speed of the particle will remain constant.

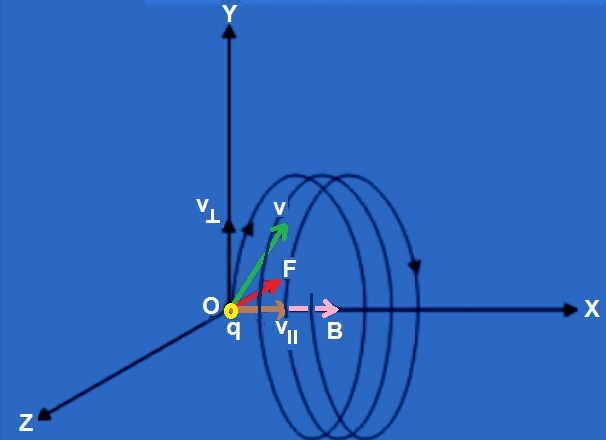
Taking                                                                         F = m·v_ￌ²/ R   

(being R the radius of curvature in the plane perpendicular to the magnetic field)

From (1) we have:                                                    m·v_ￌ²/ R = q·v_ￌ·B

So                                                                              m·v_ￌ = q·R·B   

Finally, the equation for the transverse momentum:   

P_ￌ = q·R·B

The value of P_ￌ of a produced particle is conserved, so is a very important parmeter to be considered. Although this calculus has been made using a classical frame, the equation is the same using relativistic conditions. 

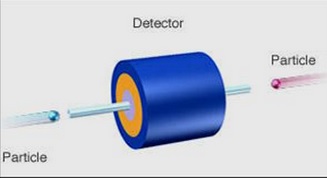
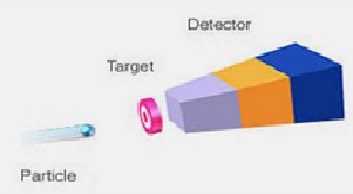
 Another interesting aspect to be considered is the difference between a head on collision and a fixed target collision.

In this case,   PT = 0  so the total energy will be used to create new particles: E = Ebeam1 + Ebeam2	In this case,     PT ≠ 0  so part of the energy will be used as kinetic energy in the new particles. E = √Ebeam
Let's talk a little bit more between a head on collision and a fixed target collision. From Special Theory of Relativity we use s a so-called Mandelstam variable, and, particularly  √s , which corresponds to the energy, in the COM frame (see here), that is available for new particle production as a result of the collision. a) fixed target collision: √s ~ √(2Ebeam·m2·c2) where m2 is de rest mass of the fixed target particle and Ebeam. is the beam proton energy. Taking a proton:  m2 ≈ 0.001 TeV/c2 To get an energy of √s = 14 TeV  (case of LHC), the proton energy in the beam should be: Ebeam ≈ 142/(2·0,001) Ebeam ~105TeV  b) head on collision: In that case √s  is: √s ~ 2√(2Ebeam1·Ebeam2) Taking two identical beams in momentum and energy Ebeam1= Ebeam2  (case of LHC) : √s = 2·Ebeam At LHC the energy required is 14 TeV, so each proton need to reach:  Ebeam =√s /2 Ebeam = 7 TeV  Looking at the both two results (7 TeV  and  105 TeV)  it is not necessary to add any comment about.