Acercándonos al LHC
|
En el LHC cada protón alcanza una energía de 7 TeV. Estamos, por tanto, en "territorio" de la Relatividad Especial. Primero presentaremos algunos cálculos básicos, y despois haremos un breve desarrollo para la Energía de colisión utilizando la mecánica relativista. Veamos el valor que toma el parámetro relativista γ (gamma) cuando el protón pose esa energía. |
|
|
En este caso la expresión para la Energía cinética es: Ek = γ·m0·c2 - m0·c2 o Ek = m0·c2(γ-1) (1) La masa en reposo del protón es 938,3 MeV/c2 Por tanto, m0·c2 = 9,383·10-4 TeV La expresión (1): 7 TeV = 9,383·10-4 (γ-1) γ ~ 7460
Como es obvio γ>>1 , por lo que estamos definitivamente en el "territorio" de la Relatividad Especial. Podemos calcular la velocidad del protón asociada a esa energía: γ = 1/[1- (v/c)2]1/2 con γ = 7460 ⇒ v = 0,999999991·c
entonces: v ~ c
|
 |
|
El uso de unidades de energía para otras magnitudes es habitual en la Física de Altas Energías. Así, la energía en reposo del protón es: E0 =m0·c2 ⇒ E0 = 1,67·10-27kg·(3·108m/s)2 ⇒ E0 = 1,503·10-10 J ⇒ E0= 938,3 MeV Dado que m0 = E0/c2 , la masa en reposo del protón puede ser expresada como m0= 938,3 MeV/c2
En unidades mas del LHC tenemos: m0=0,0009383 TeV/c2
Aunque se trata de un concepto objeto de controversia conceptual, podemos también hablar de la “masa relativista” del protón acelerado hasta la energía de 7 TeV : m = E/c2 ⇒ m = 7 TeV/c2
Comparemos este valor con el de la masa en reposo: m0=0,0009383 TeV/c2 para visualizar el incremento experimentado.
También podemos considerar el valor del momento lineal do protón en términos relativistas:
E2 = (p·c)2 + E02 ⇒ p·c = (E2 - E02)1/2 p·c = (72 - 0,00093832)1/2 ⇒ p ~ 7 TeV/c Se trata de un importante parámetro del acelerador. |
|
|
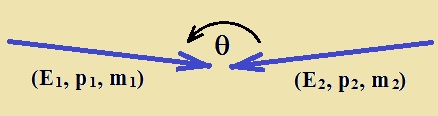
Energía en el sistema de referencia Centro-de-Momentos (COM frame). Consideremos la colisión de dos partículas con energía, momento y masa en reposo (E1, p1, m1) , (E2, p2, m2) y un ángulo de incidencia Ɵ. La siguiente cantidad es un invariante (invariante de Lorentz): s = (E1 +E2)2 - (c·p1 + c·p2)2 siendo p1 y p2 vectores y c = velocidad de la luz Operando en la ecuación anterior llegamos a: s = (E12+ E22 + 2E1·E2) - (c2p12+c2p22 + 2p1c·p2c·cosƟ) reordenando los términos: s = (E12 - c2p12) + (E22 - c2p22) + (2E1·E2 - 2p1c·p2c·cosƟ) dado que (Ei2 - c2pi2) = (mi·c2)2 tendremos: s = (m1·c2)2 + (m2 c2)2 + 2(E1·E2 - p1c·p2c·cosƟ) [1] En Física de Partículas es más común usar las llamadas “undades naturales” (c = 1) . En este caso, tendremos: s = (m1)2 + (m2)2 + 2(E1·E2 - p1·p2·cosƟ) El parámetro “s” es llamada "Mandelstam variable" y “√s” corresponde a la energía en el sistema de referencia Centro de Masas (COM frame), que es la disponible para la producción de nuevas partículas como resultado de la colisión. Blanco fijo vs Colisionador. 1.- Blanco fijo. Sea m1 la masa de la partícula proyectil y m2 la masa de la partícula que es el blanco fijo. Tenemos: p2 = 0 y E2 = m2 c2 , en el COM frame, y la ecuación [1] nos lleva a : s = (m1·c2)2 + (m2·c2)2 + 2·E1· m2 c2 Tomando en cuenta que E1 >> m1·c2 , m2 c2 , tenemos: s ~ 2E1·m2·c2
2.-Colisionador. Masa m1 y m2 en una colisión frontal (Ɵ = 180º) cosƟ = -1 y por tanto la ecuación [1] nos da: s = (m1·c2)2 + (m2 c2)2 + 2(E1·E2 + p1c·p2c) Teniendo en cuenta que Ei >> mi·c2 y E1 ~ p1·c e E2 ~ p2·c , tendremos: s ~ 2(E1·E2·+ E1·E2) → s ~ 4E1·E2
En el caso especial de partículas idénticas de igual momento, colisionando frontalmente (como es el caso del LHC), el COM frame está en reposo respecto al laboratorio, y m1 = m2 = m y E1 = E2 = E , y la ecuación [1] nos lleva a : s = (m·c2)2 + (m c2)2 + 2(E·E + 2·pc·pc) s = 2(m·c2)2 + 2·E2 + 2(p·c)2 s = 2[(m·c2)2 +(p·c)2] + 2·E2 → s = 2·E2+ 2·E2= 4·E2
Por tanto, en el caso de colisiones p-p en el LHC, con 7 TeV por protón:
Esta es la energía disponible para la producción de partículas en las colisiones p-p en el LHC. Si quisiéramos conseguir la misma energía con un Blanco fijo, considerando un proton moviéndose con energía E1 colisionando con un blanco fijo formado por un protón en reposo (m2·c2 ~ 10-3 TeV), el valor de E1 debe ser:
14 = √(2E1·10-3) E1 ~ 105 TeV Queda pues clara la ventaja de usar colisiones frontales frente a la alternativa del blanco fijo. |
|
|
Otro cálculo que podemos llevar a cabo es el dell campo magnético presente en el acelerador de otra forma a lo hecho en otra sección:
Utilizando el bending radius (rb):
rb= 2804 m Fcentripeta = Fmagnética ⇒ m·c2/rb = q·c·B
Con, E = m·c2 ⇒ B = E/(c·q·rb) y como E = 7 TeV ⇒ E = 1,12·10-6 J B = 1,12·10-6/(3·108·1,602·10-19·2804) B = 8,33 T
|
|
|
AUTORES Xabier Cid Vidal, Doctor en Física de Partículas (experimental) por la Universidad de Santiago (USC). Research Fellow in experimental Particle Physics en el CERN, desde enero de 2013 a diciembre de 2015. Estuvo vinculado al Depto de Física de Partículas de la USC como becario "Juan de la Cierva", "Ramon y Cajal" (Spanish Postdoctoral Senior Grants), y Profesor Contratado Doctor. Desde 2023 es Profesor Titular de Universidad en ese Departamento (ORCID). Ramon Cid Manzano, catedrático de Fïsica y Química en el IES de SAR (Santiago - España), y Profesor Asociado en el Departamento de Didáctica de Ciencias Experimentales de la Facultad de Educación de la Universidad de Santiago (España), hasta su retiro en 2020. Es Licenciado en Física, Licenciado en Química, y Doctor por la Universidad de Santiago (USC).(ORCID). |
CERN |
LHC |
NOTA IMPORTANTE
Toda la Bibliografía que ha sido consultada para esta Sección está indicada en la Sección de Referencias
© Xabier Cid Vidal & Ramon Cid - rcid@lhc-closer.es | SANTIAGO (ESPAÑA) |