Achegándonos ao LHC
|
No LHC cada protón acada unha enerxía de 7 TeV. Estamos, logo, en "territorio" da Relatividade Especial. Primeiro presentaremos algúns cálculos básicos e despois faremos un breve desenvolvemento para a Enerxía de colisión utilizando a mecánica relativista. Veamos el valor que toma el parámetro relativista γ (gamma) cuando el protón pose esa energía. |
|
|
Neste caso a expresión para a Enerxía cinética é: Ek = γ·m0·c2 - m0·c2 o A masa do protón é 938,3 MeV/c2 Polo tanto, m0·c2 = 9,383·10-4 TeV A expresión (1): 7 TeV = 9,383·10-4 (γ-1) γ ~ 7460
Como é obvio γ>>1 , polo que definitivamente estamos no "territorio" da Relatividade Especial. Podemos calcular a velocidade do protón asociada a esa enerxía: γ = 1/[1- (v/c)2]1/2 con γ = 7460 ⇒ v = 0,999999991·c , logo: v ~ c
|
 |
|
O uso de unidades de enerxía para outras magnitudes é habitual na Física de Altas Enerxías. Así, a enerxía en repouso do protón é: E0 =m0·c2 ⇒ E0 = 1,67·10-27kg·(3·108m/s)2 ⇒ E0 = 1,503·10-10 J Dado que m0 = E0/c2 , a masa en repouso do protón pode ser expresada como m0= 938,3 MeV/c2
En unidades máis do LHC temos: m0=0,0009383 TeV/c2
|
|
|
Aínda que se trata dun concepto obxecto de controversia conceptual, podemos tamén falar da chamada “masa relativista” do protón acelerado ata a enerxía de 7 TeV : m = E/c2 ⇒ m = 7 TeV/c2
Comparemos este valor co da masa en repouso: m0=0,0009383 TeV/c2 para ver o incremento experimentado. Tamén podemos considerar o valor do momento lineal do protón en temos relativistas:
E2 = (p·c)2 + E02 ⇒ p·c = (E2 - E02)1/2 p·c = (72 - 0,00093832)1/2 ⇒ p ~ 7 TeV/c Trátase dun importante parámetro do acelerador. |
|
|
|
|
|
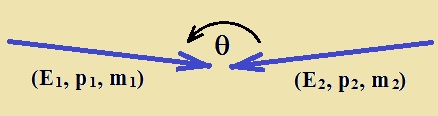
Enerxía no sistema de referencia Centro-de-Momentos (COM frame). Consideremos a colisión de dúa partículas con enerxía, momento e masa en repouso (E1, p1, m1) , (E2, p2, m2) e un ángulo de incidencia Ɵ. A seguinte cantidade é un invariate (invariante de Lorentz): s = (E1 +E2)2 - (c·p1 + c·p2)2 sendo p1 y p2 vectores e c = velocidade da luz Operando na ecuación anterior chegamos a: s = (E12+ E22 + 2E1·E2) - (c2p12+c2p22 + 2p1c·p2c·cosƟ) reordenando os termos: s = (E12 - c2p12) + (E22 - c2p22) + (2E1·E2 - 2p1c·p2c·cosƟ) dado que (Ei2 - c2pi2) = (mi·c2)2 teremos: s = (m1·c2)2 + (m2 c2)2 + 2(E1·E2 - p1c·p2c·cosƟ) En Física de Partículas é máis común usar as chamadas “undades naturais” (c = 1) . Neste caso, teremos: s = (m1)2 + (m2)2 + 2(E1·E2 - p1·p2·cosƟ) O parámetro “s” é coñecido como "Mandelstam variable" e “√s” corresponde á enerxía no centro de masas (COM frame), que é a dispoñible para a produción de novas partículas como resultado da colisión. Branco fixo vs Colisor. 1.- Branco fixo. Sea m1 a masa da partícula proxectil e m2 a masa da partícula que é o branco fixo. Temos: p2 = 0 y E2 = m2 c2 , no COM frame, e a ecuación [1] lévanos a: s = (m1·c2)2 + (m2·c2)2 + 2·E1· m2 c2 Tomando en conta que E1 >> m1·c2 , m2 c2 , temos: s ~ 2E1·m2·c2 2.-Colisor. Masa m1 e m2 en colisión frontal (Ɵ = 180º) cosƟ = -1 e polo tanto a ecuación [1] dános: s = (m1·c2)2 + (m2 c2)2 + 2(E1·E2 + p1c·p2c) Tendo en conta que Ei >> mi·c2 e E1 ~ p1·c e E2 ~ p2·c , teremos: s ~ 2(E1·E2·+ E1·E2) → s ~ 4E1·E2
No caso especial de partículas idénticas de igual momento, colidindo frontalmente (como é o caso do LHC), o COM frame está en repouso respecto ao laboratorio, e m1 = m2 = m e E1 = E2 = E , e a ecuación [1] lévanos a: s = (m·c2)2 + (m c2)2 + 2(E·E + pc·pc) s = 2(m·c2)2 + 2·E2 + 2(p·c)2 s = 2[(m·c2)2 +(p·c)2] + 2·E2 → s = 2·E2+ 2·E2 = 4·E2
Esta é a enerxía dispoñible para a produción de partículas nas colisións p-p no LHC. Se quixésemos conseguir a mesma enerxía cun Branco fixo, considerando un proton movéndose con enerxía E1 colisidindo cun branco fijo formado por un protón en repouso (m2·c2 ~ 10-3 TeV), o valor de E1 debe ser: √s ~ √(2E1·m2·c2) 14 = √(2E1·10-3) E1 ~ 105 TeV Queda pois clara a vantaxe de usar colisións frontais fronte á alternativa do branco fixo. |
|
|
Finalmente, calculamos o campo magnético presente no acelerador doutro xeito ao indicado noutra sección:
Utilizando o bending radius (rb):
rb= 2804 m Fcentripeta = Fmagnética ⇒ m·c2/rb = q·c·B
Con, E = m·c2 ⇒ B = E/(c·q·rb) e como E = 7 TeV ⇒ E = 1,12·10-6 J temos: B = 1,12·10-6/(3·108·1,602·10-19·2804) B = 8,33 T
|
|
|
AUTORES Xabier Cid Vidal, Doctor en Física de Partículas (experimental) pola Universidad de Santiago (USC). Research Fellow in experimental Particle Physics no CERN, desde xaneiro de 2013 a decembroe de 2015. Estivo vencellado ao Depto de Física de Partículas da USC como becario "Juan de la Cierva", "Ramon y Cajal" (Spanish Postdoctoral Senior Grants), e Profesor Contratado Doutor. Desde 2023 é Profesor Titular de Universidade nese Departamento (ORCID). Ramon Cid Manzano, foi catedrático de Fïsica e Química no IES de SAR (Santiago - España), e Profesor Asociado no Departamento de Didáctica de Ciencias Experimentais da Facultade de Educación da Universidad de Santiago (España), ata o seu retiro en 2020. É licenciado en Física, licenciado en Química, e Doutor pola Universidad de Santiago (USC).(ORCID). |
CERN CERN Experimental Physics Department CERN and the Environment |
LHC |
NOTA IMPORTANTE
Toda a Bibliografía que foi consultada para esta Sección está indicada na Sección de Referencias
© Xabier Cid Vidal & Ramon Cid - rcid@lhc-closer.es | SANTIAGO |